Прогноз вперед на 1 единицу

Решение

Решение

I. Сводную таблицу основных статистических характеристик для одного или нескольких массивов данных можно получить с помощью инструмента анализа данных Описательная статистика. Для этого выполните следующие шаги:

1. Введите исходные данные в MS Excel.

2. В главном меню выберите Сервис->Анализ данных->Описательная статистика (если в закладке Сервис пункт Анализ данных отсутствует, то выберите Сервис-Надстройки и поставьте галочку напротив Пакет анализа) (рисунок 12)

Рис.12. Выбор надстройки “Пакет анализа”

3. Заполните диалоговое окно ввода параметров:

· Входной интервал – диапазон, содержащий анализируемые данные (3 столбца в нашем случае).

· Группирование – по столбцам.

· Метки - флажок, который указывает, содержит ли первая строка названия столбцов или нет (в нашем случае - содержит).

· Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона.

· Итоговая статистика – поставить галочку.

Рис.13. Параметры инструмента «Описательная статистика»

Результаты вычислений представлены на рисунке 14.

Рис.14. Описательная статистика

II. Матрицу парных коэффициентов корреляции можно рассчитать, используя инструмент Анализа данных Корреляция. Для этого:

1. В главном меню выбрать Сервис->Анализ данных->Корреляция

2. Заполнить диалоговое окно ввода параметров, в качестве входного интервала следует указать весь диапазон представленных данных (рисунок 15).

Рис.15. Параметры инструмента «Корреляция»

3. Результаты построения матрицы коэффициентов парной корреляции представлены на рисунке 16.

Рис.16. Матрица коэффициентов парной корреляции

Коэффициент парной корреляции между прибылью предприятия и величиной оборотного капитала имеет отрицательную величину, следовательно, между этими признаками имеет место обратная связь, т.е. при увеличении величины оборотного капитала прибыль предприятия уменьшается. Значение коэффициента невелико по абсолютной величине, следовательно, между прибылью предприятия и величиной оборотного капитала имеет место слабая связь. Эта тенденция имеет негативный характер и в качестве рекомендаций предприятию следует предложить осуществление детального анализа всех направлений использования оборотного капитала.

Коэффициент парной корреляции между прибылью предприятия и стоимостью основных средств также имеет отрицательную величину, следовательно, между этими признаками имеет место обратная связь, что также свидетельствует о необходимости анализа всех направлений финансово-хозяйственной политики предприятия.

Из матрицы парных коэффициентов корреляции видно, что между величиной оборотного капитала и стоимостью основных средств (факторами X1 и X2) существует эффект мультиколлинеарности (коэффициент корреляции между ними >0,8), следовательно, оба фактора одновременно в модель регрессии включать нельзя, один из факторов необходимо из рассмотрения исключить. Из рассмотрения исключается тот фактор, который оказывает меньшее влияние на прибыль предприятия (результативный признак).

В данной задаче из рассмотрения необходимо исключить X1, так он оказывает меньшее влияние на результативный признак (коэффициент парной корреляции между Х1 и Y меньше по модулю, чем между X2 и Y), т.е.

.

Итак, по результатам анализа матрицы парных коэффициентов корреляции в качестве факторного признака для построения однофакторной регрессии должен быть выбран фактор Х2 (стоимость основных средств).

III. С помощью инструмента анализа данных Регрессия, помимо результатов регрессионной статистики, дисперсионного анализа и доверительных интервалов, можно получить остатки и графики подбора линии регрессии, остатков и нормальной вероятности. Порядок действий следующий:

1. Для построения модели парной регрессии в главном меню выберите Сервис->Анализ данных->Регрессия

2. Заполните диалоговое окно ввода данных и параметров вывода (рисунок 17)

· Входной интервал Y – диапазон, содержащий данные результативного признака.

· Входной интервал X – диапазон, содержащий данные факторов независимого признака (так как модель однофакторная, то построим её на основе фактора X2)

· Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет.

· Константа-ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении (метку напротив параметра не ставить).

· Выходной интервал – достаточно указать левую верхнюю ячейку диапазона с выходными данными регрессионного анализа.

Рис.17. Параметры инструмента «Регрессия»

Результаты регрессионного анализа представлены на рисунке 18.

Рис.18. Результаты регрессионного анализа

На основании этого можно записать уравнение линейной парной регрессии:

y = 173.678 - 0.98248 * x

При увеличении стоимости основных средств (Х2) на 1 млн.руб. прибыль предприятия (y) уменьшается на 0,98248 млн.рублей, что свидетельствует о нерациональном использовании финансовых ресурсов предприятия и необходимости пересмотра направлений финансово-хозяйственной политики предприятия.

IV. Для определения точечного прогноза факторного признака (X2), необходимо воспользоваться мастером диаграмм, в качестве параметра взяв диапазон для X2 – C2:С11 (рисунок 19).

Рис.19. Выбор типа диаграммы

На полученном графике необходимо добавить линию тренда (эта процедура подробно рассмотрена в задаче 1).

Рис.20. Построение линейного тренда по факторному признаку Х2

Исходя из полученного уравнения тренда, можно рассчитать прогнозное значение фактора X2 (для следующего, 11-го, момента времени):

X2 =3,3939*11+33,933=71,2659 (млн.руб.)

Прогнозное значение стоимости основных средств (Х2) может быть отображено на рис.20).

V. Для получения прогнозного значения прибыли предприятия (результативного признака) необходимо в уравнение однофакторной регрессии подставить полученное значение прогноза стоимости основных средств (факторного признака):

y = 173.678 – 0.98248 * 71.2659 = 103.66068 (млн.руб.)

VI. Для отображения прогнозного значения результативного признака нужно воспользоваться мастером диаграмм (рисунок 21)

Рис.21 Выбор типа диаграммы

В качестве входных диапазонов необходимо взять данные для факторного признака X2 - (C2:C11), для результативного признака Y - (A2:A11), на полученном графике отразить линию тренда (рисунок 22).

Для отображения на графике прогноза прибыли предприятия (Y) необходимо:

· Выделить полученный график

· Щелкнуть на нем правой кнопкой мыши и выбрать Исходные данные

· Добавить новый ряд, и ввести прогнозные значения X и Y, рассчитанные ранее.

Рис.22. Добавление на график прогнозного значения прибыли предприятия

Окончательный вид графика будет следующий (рисунок 23).

Рис.23. Построение прогноза прибыли предприятия (Y)

Задания для самостоятельной работы к задаче 2

Вариант	Признак	Наблюдения
	Y
	X1
	X2
	Y
	X1
	X2
	Y
	X1
	X2
	Y
	X1
	X2
	Y
	X1
	X2
	Y
	X1
	X2
	Y
	X1
	X2
	Y
	X1
	X2
	Y
	X1
	X2
	Y
	X1
	X2

Задача 3

По десяти кредитным учреждениям получены данные, характеризующие зависимость объема прибыли (Y, млн.руб.) от величины доходов по кредитам (X1, млн.руб.), доходов по депозитам (X2, млн.руб.) и размера внутрибанковских расходов (X3, млн.руб.).

Y
X1
X2
X3

Требуется:

1. Осуществить выбор факторных признаков для построения многофакторной регрессионной модели.

2. Рассчитать параметры регрессионной модели. Оценить ее качество.

3. Для характеристики модели определить:

· средние коэффициенты эластичности;

· бета-коэффициенты,

· дельта-коэффициенты.

4. Оценить с помощью t-критерия Стьюдента статистическую значимость коэффициентов уравнения множественной регрессии.

5. Построить регрессионную модель со статистически значимыми факторами. Оценить ее качество.

6. Определить точечный и интервальный прогноз результативного показателя.

I. Выбор факторных признаков для построения модели осуществляется с помощью матрицы коэффициентов парной корреляции. Для её построения необходимо:

· выбрать Сервис->Анализ данных->Корреляция

· заполнить необходимые поля диалогового меню (рисунок 24)

Рис.24. Ввод параметров инструмента «Корреляция»

Результаты представлены на рисунке 25.

Рис.25. Таблица коэффициентов парных корреляций

Для выявления явления мультиколлинеарности необходимо проанализировать коэффициенты парной корреляции между факторными признаками. Если имеют место коэффициенты, значение которых по модулю больше 0,8, то, следовательно, мультиколлинеарность присутствует, и это явление необходимо устранять. Если же значения коэффициентов парной корреляции между факторными признаками, взятые по модулю, меньше величины 0,8, то явление мультиколлинеарности отсутствует, и, следовательно, все факторные признаки можно включать в модель множественной регрессии.

Так как , т.е. между факторными признаками X1 и X3 существует явление мультиколлинеарности, то для построения модели выбираем тот факторный признак, который оказывает большее влияние на результативный признак (фактор, для которого коэффициент парной корреляции с результативным признаком, взятый по модулю, является большим).

Следовательно, фактор X3 оказывает большее влияние на результативный признак (Y) и этот фактор рекомендуется в модели оставить. Фактор X1 оказывает меньшее влияние на результативный признак (Y) и этот фактор рекомендуется из модели исключить.

Таким образом, для построения модели множественной регрессии выбираются два факторных признака - Х2 (величина доходов по депозитам) и Х3 (величина внутрибанковских расходов).

II. Расчет параметров регрессионной модели можно осуществить с помощью инструмента анализа данных Регрессия (см. задача 2), отличие заключается в том, что в качестве диапазона значений фактора X необходимо указать диапазон значений факторов X2 и X3 (рисунок 26).

Рис.26. Ввод параметров регрессии

Результаты построение множественной регрессии представлены на рисунке 27.

Рис.27. Вывод итогов регрессии

На основании полученных данных можно записать уравнение множественной регрессии

Y=-16,2872 + 0,197247*X2 + 0,592429*X3

Оценим качество построенной модели множественной регрессии по следующим направлениям:

· Коэффициент детерминации = 0.794176 достаточно близок к 1, следовательно, качество модели можно признать высоким.

· Критерий Фишера F = 13,50486 > Fтабл = 4,74, следовательно, уравнение регрессии признается статистически значимым и может быть использовано для анализа и прогнозирования экономических процессов.

Для вычисления Fтабл необходимо определить:

- степень свободы числителя m=2 (число факторных признаков);

- степень свободы знаменателя n-m-1=10-2-1=7;

- уровень значимости =0,05.

III. Оценим качество построенной модели множественной регрессии с помощью коэффициентов эластичности, b - и D - коэффициентов.

Коэффициент эластичности определяется:

, (1)

где - среднее значение соответствующего факторного признака,

- среднее значение результативного признака.

b_i – коэффициенты регрессии соответствующих факторных признаков.

ß-коэффициент определяется по следующей формуле:

, (2)

где - среднеквадратическое отклонение (СКО) соответствующего факторного признака (рассчитывается как корень квадратный из дисперсии признака),

- СКО результативного признака.

∆-коэффициент определяется по следующей формуле:

, (3)

где 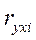- коэффициент парной корреляции результативного и соответствующего факторного признаков,

- коэффициент детерминации.

На рисунке 28 представлены формулы расчетов описанных выше коэффициентов

Рис.28. Формулы расчетов коэффициентов

Результаты вычислений представлены в таблице 2.

Таблица 2

Результаты расчета бета-, дельта- и коэффициентов эластичности

	Y	X2	X3
Ср.знач	47,8	59,4	88,4
Эласт.		0,245114	0,881663
Дисп	134,6222	67,6	247,8222
СКО	11,60268	8,221922	15,74237
bi		0,197247	0,592429
		0,139774	0,803801
		0,599604	0,883761
		0,105529	0,894471

Выводы:

· Частный коэффициент эластичности показывает, на сколько процентов изменится среднее значение результативного признака, если среднее значение конкретного факторного признака изменится на 1 %, т.е., при увеличении на 1% величины доходов по депозитным операциям (Х2) прибыль банка увеличится на 0,245 % (Э2 = 0,245), при увеличении на 1% размера внутрибанковских расходов (X3) объём прибыли увеличится на 0,88% (Э3 =0,881).

· β-коэффициент показывает, на какую величину изменится СКО результативного признака, если СКО конкретного факторного признака изменится на 1 единицу, т.е. при увеличении на 1 единицу СКО доходов по депозитам (X2), СКО объёма прибыли увеличится на 0,14 ( =0,139774); при увеличении на 1 единицу СКО внутрибанковских расходов СКО прибыли организации увеличится на 0,804 единицы ( = 0,803801).

· ∆-коэффициент показывает удельный вес влияния конкретного факторного признака в совместном влиянии всех факторных признаков на результативный показатель, т.е. удельный вес влияния внутрибанковских расходов (X3) на объём прибыли (результативный признак) составляет 89,4% (∆3 = 0,8944), а удельное влияние доходов по депозитам (Х2) на прибыль составляет 10,5 % (∆2 = 0,1055).

IV. Для оценки статистической значимости факторных признаков модели множественной регрессии используется t-критерий Стьюдента.

С помощью функции СТЬЮДРАСПОБР(0,05;7) определим табличное значение t табл = 2,364624.

Сравним расчетные значения t-статистики, взятые по модулю, с табличным значением этого критерия (расчетные значения берутся из столбца t-статистика таблицы 3 регрессионного анализа).

Таблица 3

Результаты регрессионного анализа

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересечение	-16,2872	14,93646	-1,090434022	0,311629	-51,6064	19,0319	-51,6064	19,0319
X2	0,197247	0,295027	0,668573305	0,525194	-0,50038	0,894874	-0,50038	0,894874
X3	0,592429	0,154086	3,844787137	0,006335	0,228073	0,956786	0,228073	0,956786

· t _х2 = 0,668573 < t_таб=2,364624, следовательно, фактор Х₂ признается статистически не значимым. Такой фактор из модели рекомендуется исключить.

· t _х3 = 3,844787 > t_таб=2,364624, следовательно, фактор Х₃ признается статистически значимым и информативным. Такой фактор рекомендуется в модели регрессии оставить.

V. Построим регрессионную модель со статистически значимыми факторами. Для конкретного примера статистически значимым фактором является только фактор Х3 (величина внутрибанковских расходов). Подробное построение регрессионных моделей рассмотрено ранее. Осуществим следующие установки в окне Регрессия (рисунок 29).

Рис.29. Диалоговое окно Регрессия

Получим следующие результаты (рисунок 30)

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,883761
R-квадрат	0,781033
Нормированный R-квадрат	0,753663
Стандартная ошибка	5,758688
Наблюдения
Дисперсионный анализ
	df	SS	MS	F	Знач. F
Регрессия		946,3001	946,3001	28,53526	0,000693
Остаток		265,2999	33,16248
Итого		1211,6
	Коэфф.	Стандарт. ошибка	t-статист.	P-Знач.	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересечение	-9,78049	10,93189	-0,89467	0,397079	-34,9895	15,4285	-34,9895	15,4285
X3	0,651363	0,121936	5,341841	0,000693	0,370178	0,932548	0,370178	0,932548

Рис.30. Вывод итогов регрессии

Запишем уравнение зависимости прибыли организации от величины внутрибанковских расходов (Х3):

Y = 0,651363*Х3 – 9,78049

Качество этой модели может быть оценено по коэффициенту детерминации =0,781, следовательно, размер прибыли кредитных организаций на 78,1 % зависит от величины внутрибанковских расходов.

При сравнении качества регрессии y = f (X3) с качеством регрессии
y = f (X2, X3), имеющей =0,794, можно утверждать, что улучшение качества модели не произошло.

Значение F-критерия Фишера составляет 28,53 > Fтабл (1,8)=5,32, следовательно, построенное уравнение регрессии признается статистически значимым и может быть использовано для анализа и прогнозирования процессов.

VI. Построение точечного прогноза прибыли кредитного учреждения (результативного показателя) может быть осуществлено по уравнению множественной регрессии, построенной в пункте 4 задачи, или по уравнению регрессии, содержащего только статистически значимые факторы (пункт 5 задачи).

Воспользуемся уравнением множественной регрессии, так как качество этой модели признано лучшим:

Y=0,197247*X2+0,592429*X3-16,2872

Для построения точечного прогноза результативного признака необходимо рассчитать точечные прогнозы факторных признаков (величины доходов организации по депозитам и величины внутрибанковских расходов). Для этого построим графики X2(t), X3(t) и тренд по каждому из факторов (рисунок 31,32).

Рис. 31. Выбор типа диаграммы

Рис.32. Выбор источника данных

На полученной диаграмме необходимо добавить линию тренда:

Диаграмма->Добавить линию тренда.

В настройках тренда в закладке Параметры указать (рисунок 33):

Дата добавления: 2017-02-01