
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Перетворення площин загального
|
|
|
|
Тема 3. Перетворення комплексного креслення
План
1. Метод заміни площин проекцій.
2. Перетворення площин загального положення в площину рівня.
3. Аксонометричні проекції.
Рекомендована література:
[1, с. 29-32,76-83], [3, с. 48-52, 123-133].
Міні-лексикон:
метод заміни площин проекцій; метод обертання; коефіцієнт спотворення; прямокутна ізометрія; прямокутна диметрія; косокутна фронтальна ізометрія; косокутна горизонтальна ізометрія; косокутна фронтальна диметрія.
1. Метод заміни площин проекцій
Чотири основні метричні задачі:
Ø перетворення прямої загального положення у пряму рівня;
Ø перетворення прямої загального положення у проектуючу;
Ø перетворення площини загального положення у проектуючу;
Ø перетворення площини загального положення у площину рівня
Методи перетворення:
Ø Метод заміни площин проекцій;
Ø Плоско паралельне переміщення;
Ø Обертання навколо прямих рівня;
Ø Обертання навколо проектуючих прямих;
Ø Обертання навколо сліду площини;
Ø Комбіноване перетворення комплексного креслення
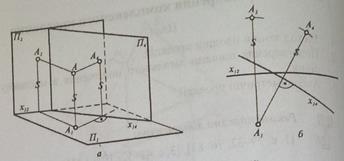
Рис. 35. Заміна площин проекцій
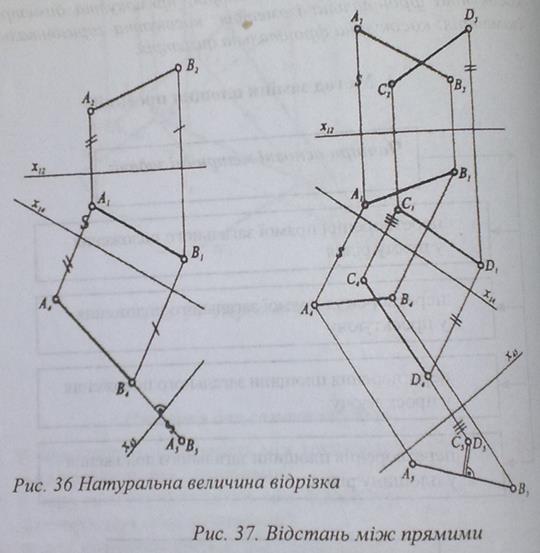
положення у площину рівня
Натуральна величина трикутника знайдена на рис. 38. Спочатку трикутник поставлено у проектуюче положення. Для цього у ньому проведено горизонталь AD і перпендикулярно до горизонтальної проекції горизонталі проведено площину П4, а потім паралельно лінійній проекції трикутника проведено П5. Натуральна величина трикутника -  ABC.
ABC.

Рис. 38. Перетворення площин загального положення у площину рівня
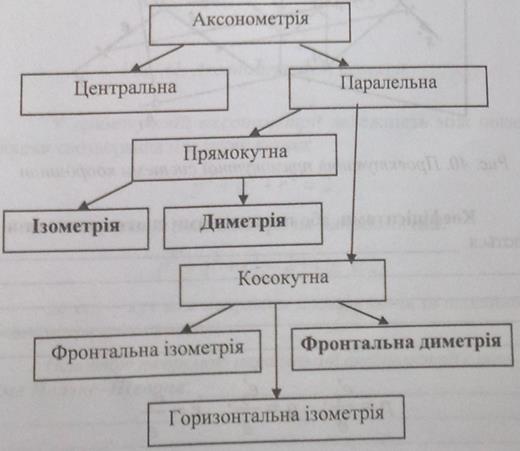
3. Аксонометричні проекції
Ідея аксонометрії полягає у тому що об'єкт жорстко прив'язується до просторової декартової системи координат, яка разом з об'єктом проектується на площину аксонометричних проекцій.
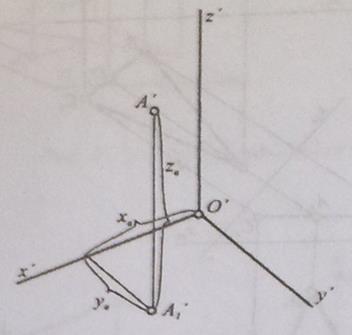
Рис. 39. Положення точки у прямокутній декартовій системі координат
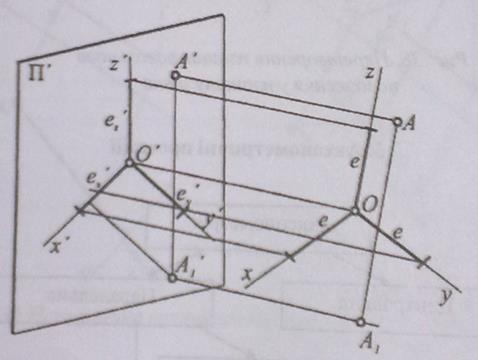
Рис.40. Проектування прямокутної системи координат
Коефіцієнтами або показниками спотворення називаються –_________
________________________________________________________________________________________________________________________________________
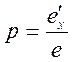
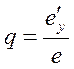


Рис. 41. Аксонометричні проекції
У прямокутній аксонометрії залежність між показниками спотворення має такий вигляд:

У косокутній аксонометрії ця залежність така:
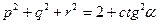 ,
,
де а — кут між напрямом проектування та площиною аксонометричних проекцій.
Основною теоремою паралельної аксонометрії є теорема Польке-Шварца –___________________________________________________________
____________________________________________________________________
Коли показники спотворення по всіх трьох осях однакові, тобто р = q = r, то аксонометрію називають ізометрією, якщо p = r  q, вона має назву диметрії, а якщо p
q, вона має назву диметрії, а якщо p  q
q  r, — триметрії. Якщо у косокутній аксонометрії показники спотворення лежать у межах від 0 до
r, — триметрії. Якщо у косокутній аксонометрії показники спотворення лежать у межах від 0 до  , тобто 0
, тобто 0 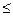 p
p 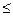
 , 0
, 0 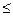 q
q 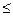
 , 0
, 0 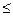 r
r 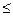
 , то у прямокутній аксонометрії 0
, то у прямокутній аксонометрії 0 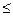 p
p 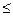 1, 0
1, 0 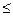 q
q 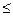 1, 0
1, 0 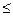 r
r 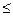 1.
1.
Приклади зображення куба із вписаними в його грані колами у найбільш поширених аксонометричних проекціях, зокрема, у прямокутній ізометрії та диметрії і косокутній фронтальній диметрії, показано на рис. 42-44.
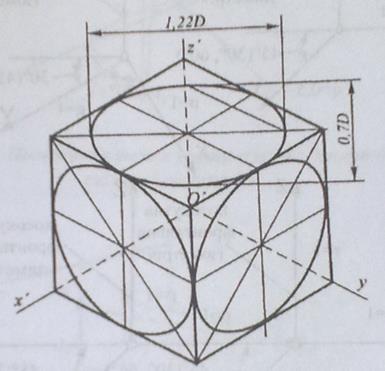
Рис. 42. Прямокутна ізометрія
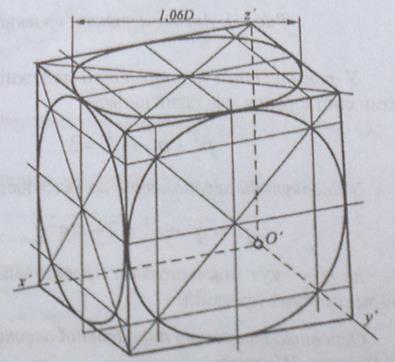
Рис. 43.Прямокутна диметрія
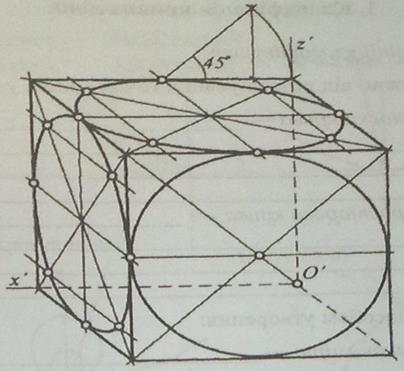
Рис. 44. Косокутна фронтальна диметрія
Питання для самоконтролю:
1. Які основні метричні задачі нарисної геометрії та інженерної графіки ви знаєте?
2. У чому полягає метод заміни площин проекцій?
3. Скільки необхідно зробити замін площин проекцій, щоб визначити натуральну величину відрізка? Щоб спроектувати відрізок у точку? Щоб визначити відстань між двома мимобіжними прямими?
4. Що таке площина рівня? Скільки необхідно зробити замін площин проекцій, щоб визначити натуральні розміри площини?
Тема 4. Проектування кривих ліній, поверхонь
План
1. Класифікація кривих ліній.
2. Класифікація поверхонь.
3. Побудова проекцій точок, що належать поверхні.
4. Перетин поверхонь з проектуючою площиною.
Рекомендована література:
[1, с. 44-61], [3, с. 60-61,68-103].
Міні-лексикон:
плоска, просторова, закономірна та незакономірна криві; січна; дотична; нормаль; гладка крива; звичайні точки; кривина дуги; особливі точки; еліпс; парабола; гіпербола; визначник поверхні; розгортувані лінійчаті поверхні; нерозгортувані лінійчаті поверхні; гвинтові поверхні; поверхні обертання.
1. Класифікація кривих ліній
Криві лінії класифікують:
1) Залежно від розташування точок кривої у просторі:
Ø плоска крива – __________________________________________________
________________________________________________________________________________________________________________________________________
Ø просторова крива – ______________________________________________
________________________________________________________________________________________________________________________________________
2) За способом утворення:
Ø Закономірні –___________________________________________________
________________________________________________________________________________________________________________________________________
v Алгебраїчні – ______________________________________________
________________________________________________________________________________________________________________________________________
v Трансцендентні – __________________________________________
________________________________________________________________________________________________________________________________________
Ø Незакономірні – _________________________________________________
________________________________________________________________________________________________________________________________________
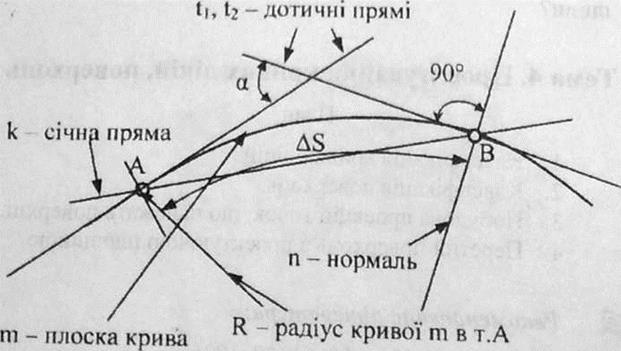
Рис. 45. Класифікація кривих ліній
Крива гладка, якщо вона у всіх своїх точках має одну дотичну що неперервно змінюється, обертаючись в одному напрямі. Точки такої кривої — звичайні точки.
Особливі точки плоских кривих:
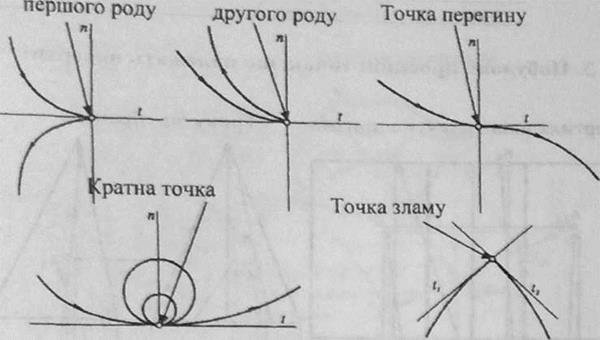
Рис.46. Особливі точки плоских кривих
2. Класифікація поверхонь
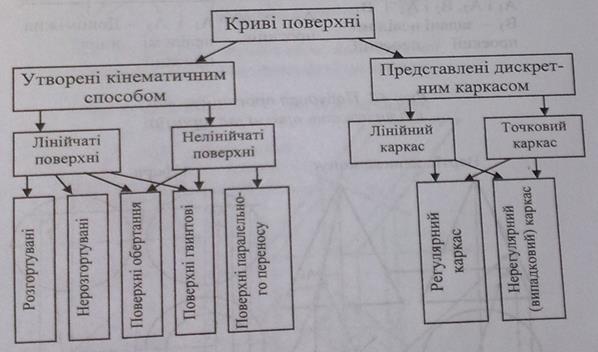
Рис.47. Класифікація кривих поверхонь
Залежно від способу утворення поверхні поділяються на:
 кінематичні – __________________________________________________
кінематичні – __________________________________________________
________________________________________________________________________________________________________________________________________
v лінійчаті;
v нелінійчаті.
 каркасні –______________________________________________________
каркасні –______________________________________________________
________________________________________________________________________________________________________________________________________
3. Побудова проекцій точок, що належать поверхні
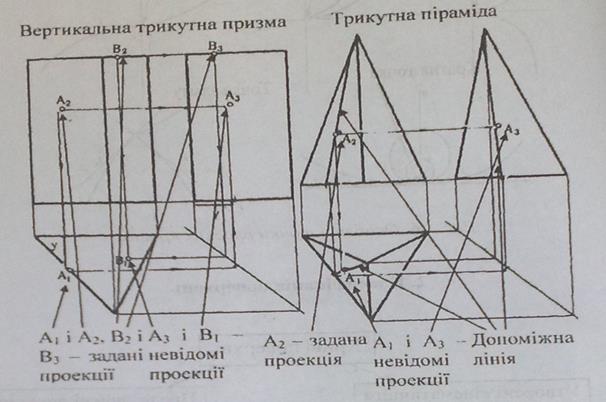
Рис. 48. Побудова проекцій точок, що належать призмі та піраміді
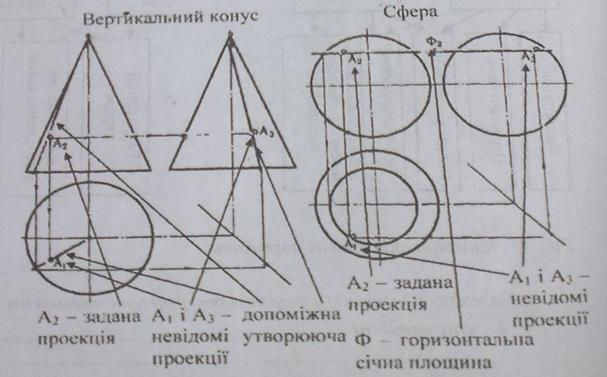
Рис. 48. Побудова проекцій точок, що належать конусу і сфері
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 59; Нарушение авторских прав?; Мы поможем в написании вашей работы!