Краткие теоретические сведения.

Задачи.

Локальная теорема Муавра-Лапласа.

Предельные теоремы для схемы Бернулли

4. Формула Бернулли удобна для вычислений лишь при сравнительно небольшом числе испытаний n. При больших значениях n пользоваться этой формулой неудобно. Чаще всего в этих случаях используют формулу Пуассона. Вероятность того, что событие наступит 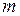раз, приближенно равна

, где .

Область применимости формулы Пуассона: n - велико, p – мало и

Вероятность того, что в условиях схемы Бернулли событие при испытаниях появится точно 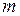раз, выражается формулой Лапласа

, где .

Область применимости: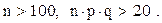

6. Интегральная теорема Муавра-Лапласа. Вероятность того, что событие появится в испытаниях от до раз (т.е. не менее и не более раз), приближенно равна

,

где ; .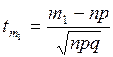

1. В классе находится 8 компьютеров. Для каждого компьютера вероятность того, что он в данный момент выключен, равна 10%. Найти вероятность того, что в данный момент: а) ни один компьютер не выключен; б) выключены 2 компьютера.

2. Вероятность приема радиосигнала при каждой передаче равна 0,86. Найти вероятность того, что при пятикратной передаче сигнал будет принят: а) 4 раза; б) не менее четырех раз.

3. Тест содержит 10 вопросов, на которые следует отвечать, используя одно из слов “Да” или “нет”. Какова вероятность получения не менее 80% правильных ответов, если использовать “метод угадывания”?

4. Из имеющихся деталей 70% стандартных и 30% нестандартных. Найти вероятность того, что из 5 взятых наудачу деталей не более одной окажется нестандартной.

5. Вероятность появления события в одном опыте равна 0,08. Чему равно наивероятнейшее число наступления события в 96 опытах?

6. Прибор состоит из 5 независимо работающих элементов. Вероятность отказа элемента в момент включения равна 0,2. Найти: а) вероятность отказа прибора, если для этого достаточно, чтобы отказало не менее четырех элементов; б) наивероятнейшее число 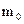отказавших элементов; в) соответствующую этому числу 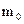вероятность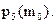

7. Вероятность выхода на линию каждого из 18 автобусов равна 0,9. Какова вероятность нормальной работы автобазы в течение дня, если для этого необходимо иметь на линии не менее 15 автобусов?

8. В равносторонний треугольник со стороной a вписан круг. Внутри треугольника независимо друг от друга выбираются пять точек. Найти вероятность того, что три из них окажутся внутри круга.

9. Считая, что в среднем 15% открывающихся в некотором регионе малых предприятий становятся в течение года банкротами, найти вероятность того, что из 10 новых малых предприятий за это время банкротами станут: а) одно; б) более трех предприятий.

10. Проводятся испытания по схеме Бернулли. Вероятность успеха в одном испытании равна . Найти вероятность события: А = {все m успехов в n испытаниях появятся подряд}

11. Сколько раз нужно подбросить игральный кубик, чтобы наивероятнейшее число выпадений двойки было равно 32?

12. Какова вероятность наступления события А в каждом испытании, если наивероятнейшее число наступления этого события в 120 испытаниях равна 32?

13. Два равносильных шахматиста играют в шахматы. Что вероятнее: а) выиграть одну партию из двух или две партии из четырех? б) выиграть не менее двух партий из четырех или не менее трех партий из пяти? Ничьи в расчет не принимаются.

14. 20 % малых предприятий терпят банкротство. Найти наивероятнейшее число обанкротившихся среди 9 предприятий.

15. Прибор состоит из трех независимо работающих элементов. Вероятности отказов элементов за время t различны и соответственно равны Найти вероятности того, что за время t откажут: а) все элементы; б) один элемент; в) два элемента; г) ни одного элемента.

16. Завод изготавливает изделия, каждое из которых должно подвергаться 4 видам испытаний. Первое испытание изделие проходит с вероятностью 0,9, второе с вероятностью 0,95, третье – с вероятностью 0,8 и четвертое с вероятностью 0,85. Найти вероятность того, что изделие пройдет благополучно: а) все 4 испытания; б) ровно 2 испытания из четырех;

в) не менее двух испытаний из четырех.

17. Вероятность сбоя в работе АТС при каждом вызове равна 0,007. Поступило 1000 вызовов. Определить вероятность 9 сбоев.

18. Завод-изготовитель отправил на предприятие по сборке компьютеров 12000 доброкачественных материнских плат. Число плат, поврежденных при транспортировке, составляет в среднем 0,05%. Найти вероятность того, что на базу поступит: а) не более трех поврежденных плат; б) хотя бы две поврежденные.

19. Вероятность выхода из строя одного элемента устройства за t часов работы равна 0,002. Какова вероятность того, что за время t из 1500 независимо работающих элементов выйдет из строя: а) 4 элемента; б) не более двух элементов.

20. Вероятность допустить ошибку при наборе некоторого текста, состоящего из 1200 знаков, равна 0,005. Найти вероятность того, что при наборе будет допущено:

а) 6 ошибок; б) хотя бы одна.

21. Садоводческий кооператив застраховал на год свои дачные дома от пожара. Каждый из 600 домовладельцев внес по 150 д.е. Вероятность пожара (в одном доме) в течение года равна 0,005, а страховая сумма, выплачиваемая пострадавшему, составляет 12000 д.е. Какова вероятность того, что страховая компания понесет убытки?

22. Вероятность того, что при автоматической штамповке изделий отдельное изделие окажется бракованным, равна 0,05. Какова вероятность того, что в партии из 1000 изделий ровно 40 бракованных?

23. Вероятность появления события в каждом из независимых испытаний равна 0,8. Сколько нужно провести испытаний, чтобы с вероятностью 0,9 можно было ожидать, что событие появится не менее 75 раз?

24. Вероятность рождения девочки равна 0,49. Какова вероятность того, что из 1000 родившихся детей девочек: а) будет 500; б) будет больше, чем мальчиков?

25. Максимальный выигрыш в игре “Спортлото” можно получить, угадав 6 из 49 номеров. В очередном розыгрыше участвуют 10 млн. карточек. Какова вероятность того, что хотя бы на одной карточке будут зачеркнуты 6 выигрышных номеров?

26. При передаче сообщения вероятность искажения одного знака равна 0,1. Найти вероятность того, что сообщение из 10 знаков: а) не будет искажено; б) содержит три искажения; в) содержит не более трех искажений.

27. На факультете обучается 500 студентов. Какова вероятность того, что 1 сентября является днем рождения: а) одного студента; б) двух студентов; в) трех студентов; г) ни одного студента?

28. Вероятность того, что расход электроэнергии в продолжение суток не превысит установленной нормы, равна . Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.

29. Прибор состоит из десяти узлов. Надежность для каждого узла равна 0,95. Узлы выходят из строя независимо друг от друга. Какова вероятность того, что откажет не более одного узла?

30. Фирма-производитель персональных компьютеров получила 500 системных блоков. Вероятность брака для партии составляет 0,035. Чему равно наивероятнейшее число бракованных системных блоков в данной партии?

31. Вероятность изготовления изделия первого сорта равна 0,8. Найти вероятность того, что среди наугад взятых 100 изделий окажется 75 первого сорта.

32. Всхожесть семян данного растения равна 0,9. Найти вероятность того, что из 900 посаженных семян число проросших заключается между 790 и 830.

33. Доля изделий высшего сорта в продукции предприятия составляет 31%. Чему равно наивероятнейшее число изделий высшего сорта в случайно отобранной партии из 75 изделий?

34. Каждый пятый клиент банка приходит в банк снимать проценты с вклада. Сейчас в банке ожидает своей очереди обслуживания шесть человек. Найти вероятность того, что из них будут снимать проценты: а) только два человека; б) хотя бы один.

35. Вероятность того, что покупателю нужен музыкальный диск, равна 0,25. Найти вероятность того, что из шести покупателей по крайней мере двум необходим музыкальный диск.

36. Вероятности выхода из строя первого, второго, третьего и четвертого приборов за время Т равны соответственно 0,2; 0,3; 0,1; 0,4. Найти вероятность того, что за время Т: а) не выйдет из строя ни один из приборов; б) выйдет из строя один, два, три, четыре прибора; в) выйдет из строя хотя бы один прибор; г) выйдет из строя не менее двух приборов.

37. При работе суперкомпьютера время от времени наблюдаются неисправности (сбои). Среднее число сбоев за сутки равно 1,5. Найти вероятности следующих событий: а) за двое суток не будет ни одного сбоя; б) в течение суток будет хотя бы один сбой; в) за неделю произойдет не менее трех сбоев.

38. В порту каждые сутки может появиться одно большегрузное судно с вероятностью 1/6. Какова вероятность того, что за месяц (30дней) порт посетят не более четырех судов?

39. При поступлении в некоторый университет вступительные экзамены в среднем выдерживают 25% абитуриентов. Предположим, что в приемную комиссию поступило 1800 заявлений. Чему равна вероятность того, что хотя бы 450 поступающих успешно сдадут экзамены?

40. Вероятность того, что пассажир опоздает к поезду, равна 0,01. Найти наиболее вероятное число опоздавших из 500 пассажиров и вероятность, соответствующую этому значению.

41. При эпидемии гриппа 40% населения заражены вирусом. В группе 24 студента. Какова вероятность того, что 10 из них будут носителями вируса?

42. По каналу связи передается n = 6 сообщений, каждое из которых независимо от других с вероятностью p = 0,2 оказывается искаженным. Найти вероятности следующих событий:

A = {ровно два сообщения из шести искажены},

B = {не менее двух сообщений из шести искажены},

C = {все сообщения будут переданы без искажений},

D = {все сообщения будут искажены}.

43. Из одной ЭВМ в другую пересылается файл объемом
10 000 символов. Вероятность ошибки при передаче символа составляет 0,001. а) определить вероятность безошибочной передачи файла; б) вычислить вероятность того, что в переданном файле будет ровно 10 ошибок;

44. Банк имеет шесть отделений. С вероятностью 0,2 независимо от других каждое отделение может заказать на следующий день крупную сумму денег. Какова вероятность того, что поступит: а) ровно две заявки; б) хотя бы одна?

45. Кандидата в высший орган Республики поддерживают 80% населения. В каких пределах с вероятностью 0,95 находится число проголосовавших «за» на выборах кандидата, если число избирателей равно 1500000?

46. В 10% случаев страховая компания выплачивает по договорам страховку. Найти вероятность того, что по истечении срока 10 договоров компания уплатит страховку в двух случаях.

47. При передаче текстовой информации слова кодируются в символы. Вероятность искажения каждого сигнала при передаче равна 0,009. При искажении двух и более символов слово не поддается шифровке. Найти вероятность того, что слово, содержащее10 символов, будет принято правильно.

Глава 2. Случайные величины и законы их распределения

2.1 Законы и функции распределения случайных величин.
Математическое ожидание и дисперсия

Случайной величиной (СВ) называют переменную величину, которая в зависимости от исходов испытания принимает значения, зависящие от случая.

Случайная величина, принимающая различные значения, которые можно записать в виде конечной или бесконечной последовательности, называется дискретной случайной величиной (принимает отдельные, изолированные значения).

Случайная величина, которая может принимать все значения из некоторого промежутка, называется непрерывной случайной величиной (число значений – бесконечно).

1) Законом распределения дискретной случайной величины называется соответствие между значениями 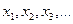этой величины и их вероятностями , т.е. совокупность пар чисел , при этом должно выполняться условие нормировки .

2) Функцией распределения случайной величины называют функцию F(x), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х: (т.е. на числовой оси лежит левее х)

а) функция распределения случайной дискретной величины:

б) функция распределения непрерывной случайной величины: , т.е. вероятность того, что случайная величина Х, заключена между и , равна разности соответствующих значений функции распределения.

График функции распределения для дискретной случайной величины представляет собой ступенчатую разрывную функцию, а непрерывной – монотонно возрастающую непрерывную функцию.

Свойства функции распределения:

1. F (–∞) = 0.

2. F (+∞) = 1.

3. F (x 1) ≤ F (x 2), при x 1 < x 2.

4. p (a ≤ X < b) = F (b) – F (a).

3) Плотность распределения вероятностей (или плотность вероятности) определяется лишь для непрерывных случайных величин.

Плотностью распределения вероятностей непрерывной случайной величины Х называется производная от ее функции распределения.

Зная плотность распределения вероятностей, можно найти функцию распределения

Свойства плотности распределения вероятностей.

1)

2)

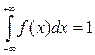
3)

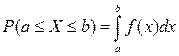
4) Математическое ожидание характеризует среднее значение случайной величины и определяется по формулам:

а) для дискретной случайной величины:

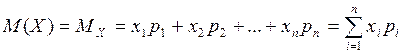, где .

б) для непрерывной случайной величины:

, где - плотность вероятности.

Свойства математического ожидания:

5) Дисперсия случайной величины характеризует степень рассеивания (разброса) значений случайной величины относительно ее математического ожидания и определяется по формулам:

а) в случае дискретной случайной величины, имеющей закон распределения .

б) для непрерывной случайной величины формула для расчета дисперсии имеет вид

Свойства дисперсии:

6) Средним квадратическим отклонением (СКО) называется корень квадратный из дисперсии случайной величины

Этот параметр также характеризует ширину диапазона значений СВ.

Дата добавления: 2017-02-01