Формулы сложения и умножения вероятностей

Задачи.

Краткие теоретические сведения

Обозначим буквой А событие «попадание случайной точки в область g, которая содержится в области G». Вероятность попадания в область g точки, брошенной в область G, определяется формулой

, где обозначает меру области (длину, площадь, объем).

1. В квадрат с вершинами в точках (0,0), (0,1), (1,1), (1,0) наудачу брошена точка. Найти вероятность того, что координаты этой точки удовлетворяют неравенству ?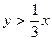

2. На отрезке [0,2] наудачу выбраны 2 числа x и y. Найти вероятность того, что эти числа удовлетворяют неравенствам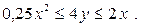

3. Два железнодорожных состава должны подойти к одному пункту разгрузки. Время прихода обоих составов независимо и равновозможно в течение суток. Определить вероятность того, что одному из составов придется ожидать освобождения пункта разгрузки, если время стоянки первого состава равно одному часу, а второго – двум часам.

4. В сигнализатор поступают сигналы от двух устройств, причем поступление каждого из сигналов не зависит друг от друга и равновозможно в любой промежуток времени длительностью 2 часа. Сигнализатор срабатывает, если интервал между моментами поступления сигналов менее 0,1 часа. Найти вероятность того, что сигнализатор сработает в течение 2 часов, если каждое из устройств пошлет по одному сигналу.

5. Какова вероятность того, что произведение двух наугад взятых правильных положительных дробей будет не больше ?

6. Какова вероятность того, что корни уравнения будут действительными, если коэффициенты p и q уравнения выбираются наудачу из отрезка [0,1]?

7. На отрезке AB длины L наудачу нанесена точка С. Найти вероятность того, что меньший из отрезков AС и CB имеет длину, большую чем L/6.

8. На паркет, составленный из правильных треугольников со стороной a, случайно падает монета радиуса r. Найти вероятность того, что монета целиком окажется внутри одного из треугольников.

9. Расстояние от пункта А до пункта В пешеход проходит за 20 минут, а автобус – за 2 минуты. Интервал движения автобусов – 30 минут. Пешеход в случайный момент времени отправляется из А в В. Какова вероятность того, что его в пути догонит автобус?

10. Плоскость разграфлена параллельными прямыми, находящимися друг от друга на расстоянии 2a. На плоскость брошена монета радиуса r < a. Найти вероятность того, что монета не пересечет ни одной из прямых.

11. Какой толщины должна быть монета радиуса R, чтобы вероятность падения на ребро была равна

12. В круг вписан квадрат. В круг наудачу бросается точка. Какова вероятность того, что точка попадет в квадрат?

13. В круг радиуса R вписан правильный треугольник. Найти вероятность того, что точка, брошенная в этот круг, попадет в данный треугольник.

14. В шар вписан куб. Точка наудачу зафиксирована в шаре. Найти вероятность того, что точка попадет в куб.

15. Два человека договорились встретиться, причем каждый из них приходит в течение одного часа и ждет 20 минут. Найти вероятность их встречи.

16. Взяты два положительных числа, каждое из которых не больше четырех. Какова вероятность того, что их сумма не превзойдет трех, а произведение будет не больше двух?

17. В прямоугольник с вершинами К(-2;0), L(-2;5), М(1;5), N(1;0) брошена точка. Какова вероятность того, что ее координаты будут удовлетворять неравенствам ?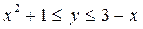

Дата добавления: 2017-02-01