Формула полной вероятности и формула Байеса

Задачи.

Формулы сложения вероятностей.

А) Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: 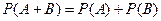. Аналогично вычисляется вероятность суммы n несовместных событий.

Б) Вероятность суммы, т.е. появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления: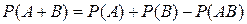

В) Вероятность суммы n совместных событий может быть рассчитана по формуле

Г) В случае, когда события А,В.С…М совместны, но независимы формула приобретает вид:

1. С первого станка поступило на сборку 300 деталей, из которых 250 стандартных, со второго 400 - из которых 350 стандартных. Найти вероятность события А, состоящего в том, что наудачу взятая деталь стандартна, и условные вероятности его относительно событи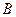й и , если событие В состоит в том, что деталь изготовлена на первом станке.

2. В коробке находится 8 отформатированных и 6 – неотформатированных дискет. Из коробки последовательно без возвращения извлекается три дискеты. Найти вероятность того, что все три дискеты неотформатированы.

3. Определить вероятность того, что партия из 50 компакт-дисков, среди которых 3 нестандартных, будет принята при испытании произвольно выбранной половины партии. Условиями приема допускается не более одного нестандартного компакт-диска из 25.

4. Вероятность поступления в институт для первого абитуриента составляет 0,85, для второго - 0,8 и для третьего - 0,7. Найти вероятность того, что хотя бы один из них поступит в институт.

5. Определить вероятность того, что наудачу взятое двузначное число окажется кратным либо двум, либо семи, либо тому и другому одновременно.

6. Чему равна вероятность того, что при n подбрасываниях игрального кубика хотя бы один раз выпадет пятерка?

7. Рабочий обслуживает четыре станка, работающих независимо друг от друга. Вероятность того, что в течение часа внимания рабочего потребует первый станок, равна 0,1, второй – 0,2, третий – 0,15 и четвертый 0,12. Какова вероятность того, что в течение часа: а) ни один станок не потребует внимания рабочего; б) все четыре станка потребуют внимания рабочего; в) какой-нибудь один станок потребует внимания рабочего; г) хотя бы один станок потребует внимания рабочего?

8. Прибор, работающий в течение суток, состоит из трех узлов, каждый из которых независимо от других может за это время выйти из строя. Неисправность хотя бы одного узла приводит к поломке прибора. Вероятность безотказной работы в течение суток первого узла равна 0,9, второго – 0,95, третьего – 0,85. Найти вероятность того, что в течение суток прибор будет работать безотказно.

9. При изготовлении детали заготовка должна пройти 4 операции. Полагая появление брака на отдельных операциях событиями независимыми, найти вероятность изготовления стандартной детали, если вероятность брака на первой операции равна 0,02, на второй – 0,01, на третьей 0,02 и на четвертой 0,03.

10. Трое рабочих последовательноизготавливают изделия, причем при передаче следующему рабочему качество изделия не проверяется. Найти вероятность выхода бракованного изделия, если первый рабочий допускает брак с вероятностью 0,04, второй – 0,05, третий 0,03.

11. Предприятие выпускает некоторое изделие, причем вероятность дефекта при выпуске равна p. После изготовления изделие осматривается последовательно k контролерами. Контролер обнаруживает дефект (если он есть) с вероятностью 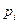. В случае обнаружения дефекта изделие бракуется. Определить вероятность событий: А - изделие будет забраковано; B - изделие будет забраковано вторым контролером; С - изделие будет забраковано всеми контролерами.

12. Завод изготавливает детали, каждая из которых может иметь дефект с вероятностью p. Деталь рассматривается одним контролером; он обнаруживает имеющийся дефект с вероятностью , а если дефект не обнаружен, - пропускает деталь в готовую продукцию. Кроме того, контролер может по ошибке забраковать деталь, не имеющую дефекта, с вероятностью a. Найти вероятности следующих событий: A – деталь будет забраковано; B – деталь будет забраковано ошибочно; С – деталь будет пропущено в готовую продукцию, но с дефектом.

13. ОТК проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,9. Найти вероятность того, что из двух проверенных изделий только одно стандартно.

14. Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,8. Найти вероятность того, что из трех проверенных изделий только два – изделия высшего сорта.

15. Среди 100 лотерейных билетов есть 5 выигрышных. Найти вероятность того, что 2 наудачу купленных билета окажутся выигрышными.

16. В коробке лежит 20% CD и 15% DVD дисков с программным обеспечением, а также CD c записями музыкальных произведений. Наудачу выбирается один диск. Какова вероятность того, что это будет диск с программным обеспечением?

17. Вероятность попасть в студенческий актив для первого студента равна 0,6, а для второго – 0,7. Найти вероятность того, что хотя бы один из них попадет в студенческий актив.

18. В цеху работают две линии сборки. Вероятность того, что в течение часа первая не потребует внимания мастера, равна 0,9, а вторая – 0,75. Найти вероятность того, что в течение часа ни одна из линий не потребует внимания мастера.

19. В каждом из трех ящиков находится по 50 деталей. В первом ящике 45 стандартных деталей, во втором - 42, в третьем – 40. Из каждого ящика наудачу вынимают по одной детали. Какова вероятность того, что все три вынутые детали окажутся стандартными.

20. Ткачиха обслуживает пять однотипных станков. Вероятность того, что любой станок в течение часа потребует внимания ткачихи, равна 0,5. Найти вероятность того, что в течение часа потребуют внимания ткачихи: а) все пять станков; б) ни один станок; в) по крайней мере один станок.

21. На склад поступило 35 холодильников. Известно, что пять холодильников с дефектами, но неизвестно – какие. Найти вероятность того, что два взятых наугад холодильника будут с дефектами.

22. Данные наблюдений показывают, что в данном районе в сентябре 10 любых дней бывают дождливыми. Совхоз должен в течение первых трех дней сентября выполнить некоторую работу. Найти вероятность того, что ни один из этих дней не будет дождливым.

23. На двух станках изготавливают однотипные изделия. Производительность первого станка в три раза выше, чем второго. Из общего числа деталей, изготовленных на двух станках за одно и тоже время, мастер берет наугад два изделия. Чему равна вероятность, что оба изделия окажутся изготовленными: а) на каком-либо одном станке; б) на различных станках?

24. Студент знает ответы на 20 вопросов из 26. Предположим, что вопросы задаются один за другим. Найти вероятность того, что три подряд заданных вопроса – счастливые.

25. Слово лотос, составленное из букв-кубиков, рассыпано на отдельные буквы, которые затем перемешаны и сложены в коробке. Из коробки наугад извлекаются одна за другой три буквы. Найти вероятность того, что при этом появится слово сто.

26. Найти вероятность того, что выбранное наудачу изделие является первосортным, если известно, что 4% всей продукции является браком, а 75% не бракованных изделий удовлетворяют требованиям первого сорта.

27. Для изучения иностранного языка группа разбивается по уровню знаний на три подгруппы. Вероятность попасть в первую подгруппу для конкретного студента равна 0,4, во вторую – 0,3. Какова вероятность попасть либо в первую, либо во вторую подгруппу?

28. На 30 одинаковых жетонах написаны числа от 1 до 30. Жетоны помещены в пакет и перемешаны. Какова вероятность вынуть жетон с номером, кратным 2 или 3?

29. В мастерской работают два электромотора. Вероятность того, что в течение часа первый электромотор не потребует внимания мастера, равна 0,9, а для второго эта вероятность равна 0,7. Найти вероятность того, что в течение часа ни один из электромоторов не потребует внимания.

30. В ящике 15 микросхем, из которых 5 первого типа и 10 - второго. Для сборки блока электронного устройства нужно сначала взять микросхему первого типа, а затем второго. Какова вероятность того, что при выборке наугад микросхемы будут взяты в нужной последовательности.

31. Сообщение передается одновременно по n каналам связи, причем для надежности по каждому каналу оно повторяется k раз. При одной передаче сообщение (независимо от других) искажается с вероятностью p. Каждый канал связи (независимо от других) «забивается» помехами с вероятностью q; «забитый» канал не может передать сообщения. Найти вероятность того, что адресат получит сообщение без искажений.

32. Вероятность безотказной работы блока в течение заданного времени равна 0,8. Для повышения надежности устанавливается такой же резервный блок. Найти вероятность безотказной работы системы с резервным блоком.

Дата добавления: 2017-02-01