Области электромагнитного излучения 1 страница

Область спектра	Длина волны λ, см	Волновое число , См^–1	Энергия Е, кДж/моль	Молекулярная причина поглощения
Микроволновая ИК дальняя ИК средняя ИК ближняя   Видимая УФ ближняя УФ дальняя	10 – 10^–1 10^–1 – 5∙10^-3 5∙10^–3 – 2∙10^–4 2∙10^–4 – 0.76∙10^–4   0.76∙10^–4–0.4∙10^–4 0.4∙10^–4 –0.2∙10^–4 0.2∙10^–4 – 10^–6	10^–1 – 10 10 – 200 200 – 5000 5000 – 13000   1.3∙10^4–2.5∙10^4 3.5∙10^4 – 5∙10^4 5∙10^4 – 10^6	0.0012 – 0.12 0.12 – 2.4 2.4 – 60 60 – 155   155 – 300 300 – 598 598 – 12000	Вращение молекул Колебания ядер и атомов в молекуле Переходы валентных электронов

Энергия молекулы (если не принимать во внимание энергию химической связи и энергию внутриядерного взаимодействия, которые не изменяются при химических и физических взаимодействиях) включает энергию поступательного движения Е_t, энергию вращательного движения E_r, энергию колебания атомов E_ν и энергию движения электронов E_el:

Из перечисленных слагаемых энергии молекулы только энергия поступательного движения может принимать любые значения, а остальные три вида энергии подчиняются квантовым законам.

Очевидно, что энергии различных видов молекулярного движения не могут быть одинаковы и должны заметно различаться. Электронная энергия значительно больше энергии колебательного движения, которая, в свою очередь, на порядок превышает энергию вращения молекулы:

Отсюда можно сделать два важных вывода. Во-первых, несмотря на то, что все виды движения в молекуле взаимосвязаны и совершаются одновременно, каждый вид молекулярного движения в первом приближении можно рассматривать независимо от другого, поскольку величины их энергии существенно различаются между собой. Во-вторых, для возбуждения того или иного вида движения, т.е. для перевода молекулы с одного (низшего) энергетического уровня на другой (более высокий) энергетический уровень, требуется совершенно различная энергия: менее всего необходимо затратить энергии для возбуждения вращательного вида движения, заметно больше для возбуждения колебательного движения и несоизмеримо больше на возбуждение электронов. Энергия электромагнитного излучения в видимой и УФ-областях соизмерима с электронной энергией молекулы, в ближней и средней ИК-областях она имеет тот же порядок, что и энергия колебания ядер в молекуле, а в дальней ИК и микроволновой областях – соответствует энергии вращения молекулы.

Из изложенного становится понятным, что спектр поглощения вещества должен заметно меняться в зависимости от того, в какой области частот (длин волн) электромагнитного излучения он получен. Существенные различия в виде спектра наблюдаются также при изменении агрегатного состояния вещества, т.е. при переходе от твердого состояния вещества к жидкому и от жидкого к газообразному.

В зависимости от того, в какой области электомагнитного излучения изучается спектр, его называют ультрафиолетовым, видимым, инфракрасным или микроволновым. Спектры в первых трех областях, обычно, называют оптическими, так как их объединяют общие способы получения и экспериментальные методы, разработанные ещё на ранней стадии развития спектроскопии для видимой области.

1.1.3. Закон светопоглощения Ламберта–Бугера–Беера

Возьмем кювету (сосуд для спектральных измерений) (рис. 1.1) с толщиной поглощающего слоя l. Заполним её каким-либо веществом. Это может быть газ, жидкость или твёрдое тело, индивидуальное вещество или раствор.

При прохождении через кювету с изучаемым веществом толщиной l параллельного монохроматического пучка света его интенсивность уменьшается. Закон светопоглощения утверждает, что ослабление светового потока в данной поглощающей среде зависит от толщины поглощающего слоя (l) и от концентрации поглощающих частиц (c). Первую зависимость часто называют законом Ламберта–Бугера: каждый тонкий слой постоянной толщины внутри однородной среды поглощает одинаковую долю падающего на него светового потока. Вторая зависимость носит название закона Беера: поглощение света данным тонким слоем внутри однородной среды пропорционально числу поглощающих частиц в единице объёма, т.е. концентрации. Обе эти зависимости обычно объединяют в одно уравнение и называют законом светопоглощения Ламберта–Бугера–Беера. Математически закон светопоглощения описывается следующим уравнением:

или

Таким образом, при прохождении монохроматического света через поглощающую среду его интенсивность уменьшается в зависимости от толщины поглощающего слоя (l) и концентрации поглощающего вещества (c) по экспоненциальному закону.

На практике приходится, однако, учитывать, что ослабление светового потока в кювете происходит как в результате поглощения, так и в результате рассеяния и отражения, особенно при прохождении пучка через границу раздела фаз у стенок кюветы (рис. 1.1).

Рис. 1.1. Ослабление светового потока в кювете с поглощающим веществом (а) и в кювете сравнения (б)

Если пропустить свет через такую же кювету, но заполненную непоглощающей средой (например, прозрачным растворителем в случае исследования раствора), то в ней ослабление светового потока произойдет только из-за рассеяния и отражения от окошек кюветы. Таким образом, для учёта собственной поглощающей способности вещества необходимо сравнивать световой поток I, прошедший через кювету с поглощающим веществом (рис. 1.1а), и световой поток I ₀, прошедший через кювету сравнения (рис. 1.1б):

или

Переходя к десятичным логарифмам и вводя обозначение

,

получаем

(1.1)

Величину A называют оптической плотностью (экстинкцией, погашением), а дробь – коэффициентом погашения (коэффициентом экстинкции).

На основании уравнения (1.1) можно дать следующую формулировку объединённого закона светопоглощения Ламберта–Бугера–Беера: при данной длине волны оптическая плотность прямо пропорциональна концентрации поглощающих частиц и толщине поглощающего слоя.

Оптическая плотность обладает свойством аддитивности, т.е. оптическая плотность смеси веществ, подчиняющихся закону светопоглощения и не вступающих в химическое взаимодействие друг с другом, равна сумме оптических плотностей компонентов при l = const:

,

где ε _i и с_i коэффициент погашения и концентрация i-го компонента смеси, соответственно.

При использовании молярной концентрации коэффициент называют молярным коэффициентом погашения. Очевидно, что по своему физическому смыслу коэффициент погашения соответствует величине оптической плотности при единичной толщине поглощающего слоя и единичной концентрации поглощающего вещества. Таким образом, по определению коэффициент погашения не может зависеть от толщины и концентрации поглощающей среды.

Кроме величины оптической плотности на практике часто используют величину пропускания (T), которая представляет собой долю света, не поглощённого системой, при его прохождении через кювету с веществом. Пропускание обычно выражают в процентах (отсюда название – процент пропускания):

(%)

Оптическая плотность и пропускание связаны между собой соотношением:

Коэффициент погашения ε зависит от природы поглощающей среды, длины волны падающего света и температуры, а величины оптической плотности (A) и пропускания (T, %) зависят кроме того ещё от концентрации и толщины поглощающего слоя.

На рис. 1.2 изображены способы графического представления законов светопоглощения.

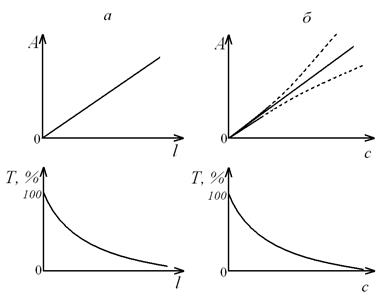
Рис. 1.2. Графическое представление законов светопоглощения при λ=const;

а – закон Ламберта–Бугера (с=const); б – закон Беера (l=const); пунктир – отклонения от закона Беера

Наблюдаемые иногда на практике отклонения от закона Беера (рис. 1.2б) могут быть вызваны либо физико-химическими, либо инструментальными причинами.

Физико-химические причины включают в себя все явления, связанные с изменением состояния поглощающих частиц при изменении концентрации, вследствие чего истинная концентрация поглощающих частиц отличается от общей концентрации вещества в растворе. Чаще всего это связано с процессами диссоциации, ассоциации, полимеризации или комплексообразования в растворах.

Инструментальные причины связаны с особенностями устройства и работы спектрофотометров и в основном сводятся к двум факторам: недостаточно строгой монохроматичности светового потока и недостаточной точности работы приёмников излучения. Чтобы снизить влияние несовершенства приёмного устройства, рекомендуется работать в интервале оптических плотностей, где ошибка в измерении будет наименьшая. Обычно удовлетворительные по точности результаты можно получать в диапазоне оптических плотностей А = 0.2–0.8. Тем не менее для каждого конкретного прибора этот интервал необходимо уточнить на основании экспериментальных исследований.

1.1.4. Вращательные спектры поглощения двухатомных молекул

Чисто вращательные спектры поглощения вещества наблюдаются в далекой ИК и микроволновой областях для веществ в газообразном состоянии. Это связано с тем, что энергии поглощаемого кванта света в этих областях достаточно только для возбуждения вращательного движения и недостаточно для перевода молекулы на более высокий колебательный энергетический уровень. Тогда в результате поглощения кванта света происходит изменение лишь вращательного энергетического состояния молекулы:

, (1.2)

а частота поглощенного кванта света соответствует частоте линии в спектре:

(1.3)

Вращательный спектр поглощения двухатомного газа (рис.1.3) представляет собой набор узких линий. Интенсивность линий в спектре проходит через максимум, причем разность волновых чисел между соседними линиями сохраняется приближенно постоянной почти на всем протяжении спектра.

Рис. 1.3. Вращательный спектр поглощения HF при 298 К

При анализе вращательного движения молекулы, в соответствии с классической механикой, используется модель "жёсткого ротатора", для которого равновесное межъядерное расстояние (r_e) и момент инерции (I_e) остаются постоянными независимо от скорости и энергии вращения. Вращательная энергия молекулы (E_r) вокруг какой-либо оси вращения прямо пропорциональна квадрату угловой скорости вращения (ω):

Подстрочный индекс " e " (equilibrium) указывает, что рассматриваемые величины относятся к равновесной конфигурации молекулы.

Для двухатомной молекулы имеются два равных по величине момента инерции относительно двух взаимно перпендикулярных осей, не совпадающих с осью молекулы: I_z = I_у = I_e, которые равны

, (1.4)

где μ – приведённая масса молекулы – это такая эквивалентная масса, которая, будучи помещена на расстояние r_e от оси вращения, приводит к той же величине момента инерции, что и две массы m ₁ и m ₂ на расстоянии r_e. Приведённая масса выражается через массы ядер m ₁ и m ₂:

, (1.5)

где А ₁ и А ₂ – атомные массы ядер, а численный коэффициент перед дробью осуществляет перевод атомных единиц массы в кг.

Момент инерции I_x равен нулю из-за чрезвычайно малых собственных размеров ядер ():

Для квантово-механического описания вращательных энергетических состояний двухатомной молекулы необходимо составить и решить уравнение Шредингера. При решении этого уравнения получается следующее выражение для собственных значений вращательной энергии E_r вокруг одной оси двухатомной молекулы:

, (1.6)

где J – вращательное квантовое число, принимающее значения 0, 1, 2, 3….

Если разделить правую и левую части уравнения (1.6) на , получим соотношение для вращательного терма F(J), выраженного в единицах волновых чисел:

Величина , содержащая одну индивидуальную константу I_e, называется вращательной постоянной данной двухатомной молекулы и обозначается В_е, т.е.:

(1.7)

Распределение молекул по вращательным квантовым уровням при данной температуре носит статистический характер и обеспечивается тепловым движением молекул. При изменении температуры заселенность вращательных уровней меняется. Чем выше температура, тем более высокие энергетические уровни заселены. Взаимное расположение вращательных уровней и их заселённость при данной температуре зависят от момента инерции молекулы. Чем больше момент инерции, тем меньше величина В_е и тем ближе друг к другу располагаются вращательные уровни.

Рассмотрим, как возникает вращательный спектр поглощения двухатомной молекулы, приведенный ранее на рис. 1.3. При поглощении квантов света в микроволновой или дальней ИК-области происходят переходы молекулы на более высокие вращательные энергетические уровни. При этом переходы не могут быть любыми. Согласно правилам отбора вращательное квантовое число изменяется на +1 при поглощении и на –1 при испускании кванта света, т.е. в общем случае:

В соответствии с этим, при поглощении кванта света, переход J"→J' возможен только между соседними уровнями, т.е. возможны переходы 0 → 1, 1 → 2, 2 → 3 и т.д.

Изменение энергии при вращательном переходе равно разности энергий верхнего и нижнего состояния: , а волновые числа вращательных переходов определяются разностью вращательных термов.

Пусть , тогда и волновые числа вращательных переходов можно выразить уравнением:

Это и есть уравнение волновых чисел вращательного спектра поглощения, из которого следует, что первая линия (J =0) лежит при волновом числе 2 В_е, вторая – при 4 В_е, третья – при 6 В_е и т.д. Таким образом, вращательный спектр поглощения двухатомной молекулы, рассматриваемой как жёсткий ротатор, должен представлять собой серию равноотстоящих линий, а разность между соседними линиями спектра , что и наблюдается на опыте (рис. 1.3).

Интенсивность каждой линии в спектре поглощения пропорциональна числу молекул на том уровне, с которого происходит переход. Заселенность же энергетических уровней для данной молекулы определяется распределением Максвелла–Больцмана, которое для вращательного движения проходит через максимум с ростом квантового числа.

Точные измерения показывают, что при увеличении волнового числа линии вращательного спектра слегка сходятся. Это вызвано тем, что заложенная во вращательное движение реальной молекулы модель жёсткого ротатора является приближенной. При больших скоростях вращения расстояние между атомами молекулы увеличивается из-за действия центробежных сил. В результате увеличивается момент инерции, а вращательная постоянная согласно (1.7), напротив, уменьшается. Как следствие, расстояние между соседними линиями во вращательном спектре также уменьшается. Отметим, что поправка на центробежное растяжение существенна лишь при больших величинах вращательного квантового числа J.

Чисто вращательный спектр наблюдается только для молекул, которые обладают постоянным дипольным моментом Р. Отсюда следует, что чисто вращательные спектры поглощения можно наблюдать только для гетероядерных молекул (HСl, СО, NО и т.п.). Все же гомоядерные двухатомные молекулы (О₂, Н₂, С1₂ и т.п.) не способны поглощать в далекой ИК и микроволновой областях спектра из-за отсутствия постоянного дипольного момента.

1.1.5. Понятие о вращательных спектрах поглощения

многоатомных молекул

В общем случае для многоатомных молекул необходимо учитывать все три главных момента инерции относительно трех осей координат. Главные моменты инерции в литературе нередко обозначаются как I_A, I_B и I_C, причем обозначение вводится так, чтобы соблюдалось условие: . Им соответствуют вращательные постоянные .

В зависимости от соотношения величин моментов инерции при анализе вращательных спектров многоатомных молекул последние подразделяют на 4 основных типа.

Линейные молекулы (HCN, N₂O). Линейные молекулы обладают только двумя вращательными степенями свободы, соответствующими вращению относительно двух взаимно перпендикулярных осей Y и Z. Так как все ядра лежат на оси OX, в соответствии с принятыми выше обозначениями, можно записать, что I_x = I_A = 0; I_y = I_z = I_В ≠ 0.

Квантовомеханическое выражение для энергии вращения в рассматриваемом случае не отличается от уравнения (1.6) для вращательной энергии двухатомной молекулы. Диаграмма вращательных энергетических уровней для линейных многоатомных молекул аналогична диаграмме для двухатомных молекул. Сохраняются те же правила отбора при вращательных переходах и внешний вид вращательного спектра, при условии, конечно, что данная молекула активна в микроволновой или дальней инфракрасной области, т.е. обладает дипольным моментом.

Молекулы типа сферического волчка (CH₄, CCl₄, SF₆). Для этих молекул главные моменты инерции относительно трёх пространственных осей координат равны и обозначаются обычно как I_B. Сюда относятся молекулы тетраэдрического и октаэдрического строения. Вращательные энергетические уровни молекул такого типа определяются тем же уравнением (1.6), что и для двухатомных молекул.

Молекулы типа симметричного волчка (NH₃, CHCl₃, C₆H₆). Для молекул этого типа два момента инерции (относительно осей X и Y) равны между собой, и отличаются от третьего (относительно оси Z). Вращательный терм таких молекул описывается более сложным выражением, которое включает два вращательных квантовых числа J и K и содержит две вращательные постоянные A и B:

Молекулы типа асимметричного волчка (H₂O, C₂H₃Cl, CH₃OH). Это наиболее общий случай. Выражение (1.6) для E_r ещё более усложняется, приходится вводить три вращательные постоянные. Вращательные спектры поглощения таких молекул чрезвычайно сложны.

Вращательные спектры поглощения многоатомных молекул (как и для двухатомных молекул) наблюдаются только в том случае, если молекулы обладают постоянным дипольным моментом. По этой причине линейные симметричные молекулы (например, CO₂, CS₂, C₂H₄), все молекулы типа сферического волчка и некоторые молекулы типа симметричного волчка (например, C₆H₆) не дают чисто вращательных спектров поглощения. Вращательные переходы неполярных многоатомных молекул можно наблюдать при анализе колебательных переходов в результате поглощения в средней и ближней ИК-областях, а также при изучении спектров комбинационного рассеяния.

1.1.6. Определение молекулярных констант (геометрических характеристик) из вращательных спектров поглощения

К геометрическим характеристикам молекул относятся равновесные расстояния между атомами в молекуле и углы между связями. Эти параметры представляют собой вполне определенные величины и отвечают условиям, при которых силы притяжения между ядрами уравновешиваются силами отталкивания. Для экспериментального определения молекулярных констант необходимо иметь значения моментов инерции. Для двухатомной молекулы имеется одно значение момента инерции – это значение, определяемое относительно любой из двух взаимно перпендикулярных осей Y или Z, поскольку I_x = 0.

Момент инерции двухатомной молекулы связан с вращательной постоянной B_e уравнением (1.7). Вращательную же постоянную можно найти из анализа вращательного спектра поглощения (рис. 1.3) по величине разности волновых чисел соседних максимумов поглощения . Для расчёта используют среднее значение , которое определяют в соответствии с выражением:

,

где – частота первой линии во вращательном спектре, – частота последней линии в ряду выбранных для определения , (n - 1) – число промежутков между линиями спектра в данном интервале частот

На основании полученного значения находят B_e:

(1.8)

Далее по формуле (1.7) рассчитывается величина момента инерции (кг∙м²):

(1.9)

Определение межъядерного расстояния проводят по уравнению (1.4), предварительно рассчитав по (1.5) приведенную массу (1.5):

(1.10)

В случае гомоядерной двухатомной молекулы приведенная масса оказывается вдвое меньше массы атома: . Для расчёта межъядерных расстояний в молекуле типа сферического волчка достаточно найти момент инерции относительно одной из трёх взаимно перпендикулярных осей вращения, поскольку I_x = I_y = I_z.

Рис. 1.4. Пространственная модель молекулы метана (к вычислению межъядерного расстояния r связи C–H)

Так, например, для определения межъядерного расстояния связи C–H (r на рис. 1.4) удобно выбрать ось вращения, проходящую через центры атома углерода и атома водорода (ось Z). Тогда момент инерции

,

где l – проекция межъядерного расстояния r на основание тетраэдра.

Вращательную постоянную B_e находят по разности волновых чисел соседних пиков поглощения для тонкой вращательной структры колебательно-вращательного спектра поглощения CH₄, так как чисто вращательных спектров поглощения для молекулы типа сферического волчка получить нельзя, вследствие отсутствия у молекулы CH₄ постоянного дипольного момента. Затем, аналогично тому, как это делается для двухатомных молекул, по уравнению (1.7) находят момент инерции I_B. Момент инерции для молекулы сферического волчка относительно оси симметрии равен:

, (1.11)

где угол α – угол между связью C–H и осью симметрии молекулы.

Угол между центральным атомом и атомами, расположенными в вершинах тетраэдра, т.е. угол H–C–H в молекуле метана (рис. 1.4) составляет 109^o28'. Поскольку угол является смежным с углом H–C–H, то имеем:

или (1.12)

В случае молекул симметричного волчка из спектральных данных удаётся определить только одну вращательную постоянную В и один момент инерции , относительно осей Х и Y, перпендикулярных оси симметрии волчка.

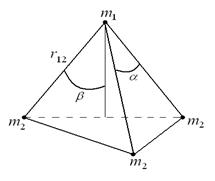
Рис. 1.5. Пространственная модель молекулы аммиака (к вычислению межъядерного расстояния r ₁₂ связи N–H).

Так, в частности, для молекулы аммиака, имеющей структуру тригональной пирамиды (рис. 1.5), моменты инерции соответственно равны:

относительно оси симметрии

(1.13)

относительно осей X и Y:

(1.14)

Из экспериментальных данных вычисляют момент инерции и далее по формуле (1.13) находят межъядерное расстояние r ₁₂ связи N–H.

В выражение для момента инерции входят не только массы ядер и межъядерные расстояния, но и межсвязевые углы (1.11)-(1.14). Это дает возможность находить последние из вращательных спектров, если межъядерные расстояния в молекуле известны или могут быть определены на основании других методов измерения. Отметим, что спектроскопические измерения позволяют определять внутримолекулярные расстояния с точностью до 10^–3 – 10^–2 нм, углы между связями – с точностью до 1 – 2^о.

Дата добавления: 2017-02-01