Области электромагнитного излучения 2 страница

1.1.7. Колебательные спектры поглощения двухатомных молекул

Поглощение в средней и ближней ИК-областях обусловлено обычно колебательными переходами при неизменном электронном состоянии молекулы; соответствующие спектры называют колебательными. Точнее их следовало бы называть колебательно-вращательными, так как изменение колебательной энергии молекулы при поглощении кванта света в этих областях сопровождается, как правило, изменением и вращательной энергии:

На рис. 1.6 приведен колебательный спектр поглощения газообразного оксида углерода. Он состоит из ряда довольно далеко отстоящих друг от друга полос, интенсивность которых с ростом волнового числа резко убывает. Первую, наиболее интенсивную полосу называют основной полосой, или основным тоном. Далее располагаются 1-й и 2-й обертоны. Интенсивность последующих полос убывает настолько резко, что уже 3-й и 4-й обертоны для большинства молекул наблюдать не удается.

Рис. 1.6. Колебательный спектр поглощения СО

Характер изображённого на рис. 1.6 спектра является типичным для гетероядерных двухатомных молекул. Каждая полоса в спектре является сложной и при записи на приборе с большой разрешающей способностью распадается на ряд отдельных линий (см. врезку на рис. 1.6). Появление такой тонкой структуры характерно для веществ в газообразном состоянии. Положение полос в спектре определяется колебательными переходами, а тонкая структура каждой полосы – вращательными переходами.

Для того чтобы понять происхождение представленного спектра, примем во внимание вначале только колебательное движение и колебательные переходы, абстрагируясь от вращения молекулы, т.е. примем, что , где , – колебательная энергия молекулы на высшем и низшем колебательных энергетических уровнях.

Колебательное движение двухатомной молекулы с точки зрения классической механики можно представить как периодическое изменение расстояния между ядрами. Пусть равновесное межъядерное расстояние в молекуле равно r_e, а общее изменение длины связи при колебании (как в сторону уменьшения, так и в сторону увеличения межъядерного расстояния) составляет (r_A + r_B) (рис. 1.7).

Рис. 1.7. Схема колебательного движения двухатомной молекулы

Тогда согласно закону Гука, который описывает гармонические колебания, сила, возвращающая ядра в положение равновесия, пропорциональна смещению ядер из состояния равновесия:

,

где – колебательная координата, k – силовая постоянная.

Силовая постоянная является важной характеристикой молекулы. Её физический смысл вытекает из условия: если q =1, то . Силовая постоянная двухатомной молекулы есть величина, характеризующая упругость связи и численно равная силе, деформирующей (растягивающей или сжимающей) связь на единицу длины.

Если двухатомную молекулу рассматривать как гармонический осциллятор, её потенциальная энергия будет описываться уравнением:

Подставляя это выражение в уравнение Шредингера и решая его, получаем выражение для собственных значений колебательной энергии двухатомной молекулы:

, (1.15)

где 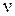– колебательное квантовое число, принимающее значения целых положительных чисел, начиная с нуля ( 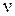=0, 1, 2, 3…); – колебательная постоянная, или собственная частота, характеризующая частоту колебаний, отнесённую к минимуму потенциальной кривой, т.е. ту частоту, которую согласно классической механике имела бы молекула для бесконечно малой амплитуды колебаний (q = 0, r = r_e).

Колебательная постоянная ω_e для гармонического осциллятора связана с силовой постоянной k следующим соотношением:

,

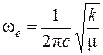где μ – приведённая масса молекулы.

Силовые постоянные двухатомных молекул имеют порядок 10² – 10³ Н/м, или ~ 0.1 - 10 мдин/Å.

Энергия колебаний гармонического осциллятора возрастает прямо пропорционально квантовому числу ν, что соответствует системе равноотстоящих квантовых уровней (рис. 1.8). Согласно квантовомеханическим правилам отбора для гармонического осциллятора возможны переходы с 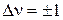. При поглощении света гармоническим осциллятором колебательное квантовое число изменяется на +1, увеличивается энергия и амплитуда колебаний.

Рис. 1.8. Кривая потенциальной энергии (а) и зависимость колебательной энергии Е_ν от квантового числа ν (б) для модели гармонического осциллятора

Применение к молекуле модели гармонического осциллятора приводит к ряду результатов, противоречащих наблюдаемым экспериментальным данным. Во-первых, для энергии гармонического осциллятора E _ν (1.15) нет ограничений и она, следовательно, может быть сколь угодно большой. В этом случае химическая связь в молекуле была бы бесконечно упругой, и её разрыв был бы невозможен. Однако, как известно, это не так. Во-вторых, для гармонического осциллятора в спектре поглощения должна наблюдаться только одна полоса, что вытекает из правил отбора и эквидистантности колебательных уровней (рис. 1.8а). В то же время опыт показывает, что в колебательном спектре реальной двухатомной молекулы наблюдается несколько полос (рис. 1.6). Всё это означает, что к реальным молекулам не применима модель гармонического осциллятора. Гармоническое приближение для них можно использовать только при малых смещениях ядер от положения равновесия, т.е. при малых значениях колебательного квантового числа (ν = 0; l).

Тем не менее, модель гармонического осциллятора позволяет оценить ряд количественных характеристик двухатомной молекулы, в частности, величину силовой постоянной и упругость химической связи. Кроме того, в некоторых случаях колебания реальных молекул в достаточно хорошем приближении можно считать гармоническими, особенно в твёрдых телах. И, наконец, гармоническое приближение является, на сегодняшний день, наиболее используемым и по существу единственным подходом при исследованиях колебательных спектров многоатомных молекул.

Для реальных двухатомных молекул функция U(r) не является параболой и возвращающая сила не строго пропорциональна величине смещения ядер. Это приводит к модели ангармонического осциллятора, для которого кривая потенциальной энергии описывается функцией Морзе (рис. 1.9):

где D ₀ – энергия диссоциации, b – постоянная для данной молекулы.

Рис. 1.9. Кривая потенциальной энергии (а) и зависимость колебательной энергии Е_ν от ν (б) для ангармонического осциллятора.

В случае модели ангармонического осциллятора колебательная энергия будет равна:

, (1.16)

где ω _ех_е – коэффициент ангармоничности, характеризующий отклонение колебаний от гармоничности, причём .

Величина ω_ех_е измеряется в тех же единицах, что и ω _е (м^–1, см^–1). Безразмерную величину х_е также иногда называют коэффициентом ангармоничности.

Из уравнения (1.16) можно получить выражение для колебательного терма:

,

а также для нулевой энергии ангармонического осциллятора:

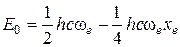
Кривая Е _ν – ν имеет максимум (рис. 1.9б) и колебательные уровни сходятся к некоторому значению ν_макс, которое можно найти из условия максимума :

откуда

(1.17)

Таким образом, существует конечное число дискретных колебательных уровней и максимальная энергия ангармонического осциллятора Е _ν,макс. Если молекуле сообщить колебательную энергию Е _ν > Е _ν,макс, произойдет диссоциация, как это видно из кривой потенциальной энергии (рис. 1.9а).

Рассчитанные по формуле (1.17) значения ν_макс для большинства молекул составляют несколько десятков, для некоторых – до полутора сотен.

Следует отметить, что уравнение (1.16) недостаточно точно описывает зависимость Е_ν от ν, особенно при больших значениях ν. Причина – в приближённом характере функции Морзе, на основании которой было получено уравнение (1.16). Отсюда вытекает и приближённый характер формулы (1.17), которая обычно дает завышенные значения ν_макс.

Для ангармонического осциллятора квантово-механические правила отбора разрешают любые переходы: Δν = ±1, ±2, ±3 и т.д.

Для большинства двухатомных молекул колебательный переход требует ~10 – 100 кДж/моль. Это значительно больше средней энергии теплового движения молекул газа при температуре опыта (18 – 25^оС) (RT 2,5 кДж/моль при 298 К), поэтому можно считать, что при этой температуре подавляющее число молекул находится на самом низшем колебательном уровне, т.е. .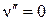

Наименьшая энергия требуется для перехода . Это соответствует появлению в спектре поглощения первой (низкочастотной) полосы – основного тона (рис. 1.6). Переходы 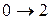, 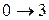и т.д. дают последующие полосы – обертоны (1-й, 2-й и т.д.).

В общем виде уравнение для волновых чисел колебательных переходов с нулевого уровня на любой уровень ν будет следующим:

,

где ν = 1, 2, 3,…,ν_макс.

С учётом этого, для волновых чисел основной полосы и первого и второго обертонов получаем:

основная полоса (основной тон)

1-й обертон (1.18)

2-й обертон

Измерив волновые числа основного тона и 1-го обертона, можно вычислить собственную частоту колебаний и коэффициент ангармоничности, а затем и важную характеристику молекулы – энергию диссоциации.

Рис. 1.10. Схема, иллюстрирующая понятие энергии диссоциации

Энергией диссоциации двухатомной молекулы называют изменение энергии Δ U ₀ (при абсолютном нуле) в результате перехода , причём и молекулы ХY и атомы X и Y находятся в состоянии идеального газа (рис. 1.10).

Продукты реакции должны быть удалены на бесконечно большое расстояние, а молекула XY должна находиться на нулевом колебательном уровне (что согласуется с условием: Т = 0).

Энергию диссоциации, отсчитываемую от нулевого уровня и отнесенную к 1 молю двухатомного газа, называют истинной энергией диссоциации и обозначают D ₀:

Если энергию диссоциации отсчитывать от минимума потенциальной кривой, то она превышает D ₀ на величину нулевой энергии

По колебательным спектрам поглощения можно рассчитать D ₀, а затем, зная Е ₀, найти D _е. Величину Е ₀, а, следовательно, и D_е, можно рассчитать только используя экспериментальные спектральные данные. Поэтому D_е часто называют спектроскопической энергией диссоциации.

Истинную энергию диссоциации D ₀ в расчете на 1 моль определяют по формуле:

,

где N_A – число Авогадро (6,023∙10²³ моль^-1).

1.1.8. Определение колебательной постоянной, коэффициента ангармоничности и энергии диссоциации двухатомной молекулы по колебательному спектру поглощения

Целью экспериментального изучения спектров поглощения двухатомных молекул в ИК-области является определение молекулярных констант – колебательной постоянной, коэффициента ангармоничности и энергии диссоциации молекулы.

Значение колебательной постоянной (собственной частоты колебаний атомов в молекуле) можно приближенно оценить по положению основного тона в колебательном спектре, так как .

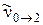Для точного определения колебательной постоянной и расчёта коэффициента ангармоничности используют систему уравнений (1.18), находя по спектру волновые числа основного тона (основной полосы) и 1-го обертона . На основе полученных значений колебательной постоянной и коэффициента ангармоничности определяют важнейшую энергетическую характеристику молекулы – энергию диссоциации.

1.1.9. Колебательно-вращательные спектры поглощения

двухатомных молекул

Если какую-либо из колебательных полос в спектре поглощения записать на приборе с большой разрешающей способностью, то она распадется на ряд отдельных линий (см. врезку на рис. 1.6). Переходы между колебательными уровнями сопровождаются, как правило, изменением и вращательного состояния молекулы. Если молекула способна поглощать электромагнитную энергию в ИК области, т.е. соблюдается условие 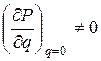(P – дипольный момент, q – заряд) возникает колебательно-вращательный спектр. Положение полос в таком спектре определяется колебательными переходами, а тонкая структура каждой полосы – вращательными переходами. Возникновение колебательно-вращательной полосы можно пояснить схемой на рис. 1.11.

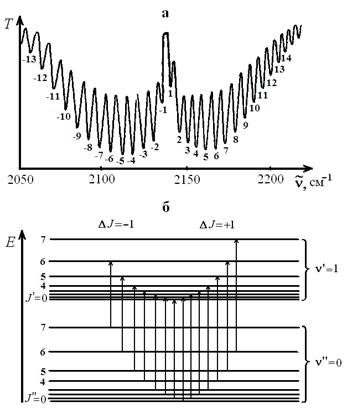
Рис. 1.11. Колебательно-вращательная полоса поглощения СО (а) и схема её возникновения (б)

Согласно правилам отбора при колебательном переходе, вследствие поглощения энергии, изменение вращательного квантового числа Δ J может быть равно не только +1, но и –1. Это позволяет разделить переходы и соответствующие им линии в полосе на отдельные группы – так называемые "ветви". Если при колебательном переходе вращательное квантовое число J изменяется на –1, совокупность соответствующих линий образует Р -ветвь полосы, а если вращательное квантовое число J изменяется на +1, образуется R -ветвь. Как видно из рис. 1.11а, R -ветвь располагается при более высоких волновых числах, чем Р -ветвь.

Между Р - и R -ветвями в спектрах двухатомных молекул наблюдается промежуток – отсутствие поглощения. Это так называемая "нулевая линия", обусловленная тем, что для большинства двухатомных молекул переходы с запрещены. Для некоторых молекул (например, NO) наряду с переходами разрешены и переходы . В этих исключительных случаях между Р - и R -ветвями появляется Q -ветвь, линии в которой расположены очень близко друг к другу и обычно сливаются в узкую полосу без различимой тонкой структуры.

Интенсивность линий внутри каждой ветви колебательно-вращательной полосы проходит через максимум, что отражает характер распределения молекул по вращательным уровням в нижнем колебательном состоянии.

Для основного тона выражения для волновых чисел переходов имеют вид:

для Р -ветви

для R -ветви

Легко видеть, что для модели жёсткого ротатора разность волновых чисел между соседними линиями спектра как в Р -, так и в R -ветви постоянна: , т.е. так же, как в случае чисто вращательного спектра. Поэтому колебательно-вращательные спектры можно также использовать для определения межъядерного расстояния молекул. Положение колебательной полосы определяется как среднее между соответствующими полосами в P - и R -ветвях.

1.1.10. Определение волнового числа колебательно-вращатель-ной полосы и молекулярных констант по вращательно-колебатель-ному спектру поглощения

Для определения волнового числа колебательно-вращательной полосы (“нулевой линии”) комбинируют сумму волновых чисел определенной пары линий, одна из которых принадлежит Р -, а другая R -ветви:

(1.19)

На практике чаще всего используют ближайшие к провалу интенсивности линии P - и R -ветвей, а именно, отвечающие условию в формуле (1.19).

Определение значений молекулярных констант (момента инерции и межъядерного расстояния) основывается на предположении о независимости вращательной постоянной от колебательного состояния молекулы . В этом случае достаточно найти среднюю разность соседних линий в Р - и R -ветвях колебательно-вращательной полосы. Обычно для определения используют 4-5 ближайших к провалу интенсивности линий в каждой из ветвей. Определенная таким образом средняя разность волновых чисел соседних линий поглощения, очевидно, будет равна . И далее по формулам (1.7) и (1.4) рассчитывают средние значения момента инерции I и межъядерного расстояния r.

1.1.11. Колебательные состояния многоатомных молекул

В отличие от двухатомных гетероядерных молекул ИК-спектр поглощения многоатомных молекул значительно сложнее. Это объясняется тем, что в отличие от двухатомных молекул, обладающих лишь одной колебательной степенью свободы (колебание ядер вдоль линии химической связи), многоатомные молекулы имеют, по крайней мере, 3 колебательных степени свободы, причём с ростом количества атомов в молекуле их число увеличивается.

Число колебательных степеней свободы n в зависимости от числа атомов в молекуле N определяется по формулам:

(для линейных молекул) (1.20)

(для нелинейных молекул) (1.21)

Эти выражения обосновываются исходя из следующих соображений. Молекула одноатомного газа может иметь лишь три поступательные степени свободы, по которым равномерно распределена вся её энергия. Если молекула образована из N атомов, то эти три степени свободы сохраняются и для каждого атома, входящего в состав молекулы. Таким образом, молекула, в целом, должна обладать 3 N степенями свободы, которые распределяются по различным видам молекулярного движения. Три из них будут приходиться на поступательное движение молекулы и ещё две (для линейных) или три (для нелинейных) связаны с вращательным движением молекулы как целого. Остальные ( или ) приходятся на колебательное движение, которое сопровождается изменением формы молекулы, обусловленное её изгибом или растяжением химических связей.

Колебания ядер молекулы представляют собой достаточно сложное явление. В классическом (т.е. основанном на законах классической механики) приближении, как и в случае двухатомных молекул, колебания многоатомных молекул при малых амплитудах можно считать гармоническими. Из теории малых колебаний следует, что любое сколь угодно сложное колебательное движение молекулы в гармоническом приближении можно разложить на n независимых движений, которые называются нормальными колебаниями. Каждое нормальное колебание совершается с определенной частотой , которая называется частотой данного нормального колебания. Для частоты нормального колебания также используют названия основная или фундаментальная частота.

Для описания колебательного движения молекулы вводят, соответственно числу нормальных колебаний, или колебательных координат. В качестве таких координат удобно выбрать величины, характеризующие изменение расстояний между ядрами и изменение углов между связями (по отношению к их равновесным значениям). Такая система внутренних координат получила название валентно-силовой системы координат, а сами координаты – естественных колебательных координат q_i.

Так, например, для трехатомной нелинейной молекулы XYZ, которая имеет 3 колебательные степени свободы (), вводятся 3 колебательные координаты (рис. 1.12), две из которых отвечают изменению межъядерных расстояний XY (q ₁) и XZ (q ₂), а третья – изменению угла между связями YXZ (q ₃), т.е. молекула XYZ имеет три нормальных колебания и, следовательно, три основных частоты колебаний.

Рис. 1.12. Внутренние колебательные координаты трёхатомной молекулы: q ₁, q ₂, q ₃ = q ₃'+ q ₃''

Величина и направление амплитуд смещения ядер для данного нормального колебания определяют его форму, исходя из которой колебания разделяют на валентные (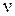) и деформационные ().

Валентными называют колебания, связанные в основном с изменением длины связей, при этом межсвязевые и другие углы остаются почти неизменными. Деформационными называют колебания, при которых в основном изменяются межсвязевые и другие углы, а длины связей практически не изменяются.

Валентные и деформационные колебания могут быть как симметричными (s), так и антисимметричными (as).

В качестве примера ниже показаны (схематически) различные колебания метиленовых (–СН₂–) групп (рис. 1.13).

Рис. 1.13. Различные формы колебательного движения метиленовых групп:

а – симметричное, б – антисимметричное, в – ножничное, г – маятниковое,

д – веерное, е – крутильное

Чисто валентные и чисто деформационные колебания встречаются редко – только для линейных или высокосимметричных молекул. Для большинства молекул характерны смешанные колебания, в которых одновременно изменяются как длины связей, так и межсвязевые и другие углы.

Для молекул с низкой симметрией возможны только невырожденные колебания. Число различных частот нормальных колебаний в этом случае равно числу колебательных степеней свободы. В более симметричных молекулах некоторые нормальные колебания различной формы совершается с одинаковой частотой. Такие колебания называют вырожденными, а число таких колебаний – степенью вырождения.

1.1.12. Общие представления о колебательных спектрах

многоатомных молекул

Число колебательных степеней свободы n для многоатомной молекулы легко подсчитать по формулам (1.20) и (1.21). Казалось бы, число основных полос в спектре поглощения вещества должно совпадать с этим числом. Эксперимент, однако, показывает, что очень часто число основных полос оказывается меньше числа внутримолекулярных колебаний. Данные табл. 1.2 иллюстрируют это на примере нескольких веществ.

Таблица 1.2.

Число колебательных степеней свободы, частот колебаний и основных полос в ИК-спектре поглощения некоторых многоатомных молекул

Молекула	Число колебательных степеней свободы	Число частот колебаний	Число основных полос
H2O CO2 NH3 CH4 CHCl3	3∙3-6=3 3∙3-5=4 3∙4-6=6 3∙5-6=9 3∙5-6=9

Несовпадение числа основных полос в спектре поглощения вещества с числом внутримолекулярных колебаний возможно по двум причинам.

Во-первых, как уже указывалось, некоторые колебания в многоатомных молекулах могут быть вырожденными. Если в молекуле несколько таких колебаний, то число различных частот по сравнению с числом колебаний будет меньше, а вся группа вырожденных колебаний даст в ИК-спектре лишь одну основную полосу. Чем выше симметрия молекулы, тем чаще встречается вырождение колебаний и тем больше будет групп вырожденных колебаний.

Во-вторых, при различных колебаниях молекула обладает разной способностью к поглощению электромагнитной энергии. Согласно классической электродинамике поглощение электромагнитной энергии должно сопровождаться изменением осцилляции электрических зарядов в поглощающей среде. Поэтому в ИК-области могут поглощать только те молекулы, у которых при изменении расстояния между ядрами происходит смещение центров тяжести электрических зарядов, т.е. колебание сопровождается изменением дипольного момента. Таким образом, колебание будет активно в ИК-области, если для него соблюдается условие:

Дата добавления: 2017-02-01