Декартові координати

Проекція вектора на вісь

Рис. 2. 4.

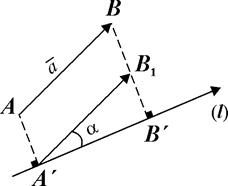Нехай – напрямлена пряма, тобто пряма, на якій задано додатний напрям. Якщо на цій прямій задано початок відліку і масштаб, вона стає числовою прямою, тобто віссю. Нехай 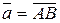– будь-який вектор (рис. 2.4). Проведемо перпендикуляри до осі з точки А (з основою ) і з точки В (з основою ).

Означення. Проекцією вектора 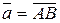на вісь називається довжина відрізка , взята з додатним знаком, якщо напрями вектора і осі однакові, і з від’ємним знаком, якщо напрями вектора і осі протилежні. Проекція вектора на вісь позначається або 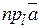. Таким чином

=

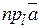Аналогічним чином визначається і проекція одного вектора на другий; в цьому разі перпендикуляри проводяться до прямої, на якій лежить цей другий вектор, а її напрямом вважається напрям цього вектора.

Відзначимо основні властивості проекцій.

1) При паралельному переносі вектора його проекція не змінюється (рис. 2.4).

2) Проекція 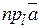= 0 тоді і тільки тоді, коли .

3) На рис. 2.4 з D бачимо, що

. (2.1)

Рис. 2.5

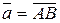Тут = α – кут між вектором та віссю . Таким чином, знак проекції визначається знаком : якщо 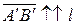, то кут 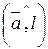гострий і косинус додатний, а якщо , то цей кут тупий і косинус від’ємний.

4) Проекція суми векторів дорівнює сумі їх проекцій (рис. 2.5):

. (2.2)

5) Числовий множник можна винести за знак проекції:

. (2.3)

Це випливає, наприклад, з формули (2.1).

З довільної точки простору О проведем три попарно перпендикулярні осі з однаковим масштабом. Точка О називається початком координат, a oci, які проходять через початок координат, називаються осями координат. Перша з них позначається Ох i називається віссю абсцис, друга вісь — Оу i називається вiccю ординат i третя — Оz — називається вiccю аплікат. Така система координат називається прямокутною або декартовою.

Площини, якіпроходять через oci координат, називаються координатними площинами. Вони поділяють пpocтip на вісім октантів.

Декартовими координатами вектора у прямокутній системі координат називаються його проекції на координатні осі.

Нехай М – будь-яка точка простору. Розглянемо вектор 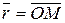– радіус-вектор цієї точки.

Координати радіус-вектора точки М, тобто числа , називаються декартовими координатами точки М, відповідно абсцисою, ординатою і аплікатою цієї точки, що записується

Рис. 2. 6 так: М .

Таким чином встановлюється взаємно однозначна відповідність між точками простору і упорядкованими трійками чисел – координат цих точок. Ця відповідність дає змогу розв’язувати геометричні задачі алгебраїчними методами, шляхом дій над координатами точок, що є предметом аналітичної геометрії.

Позначимо через вектори одиничної довжини, напрями яких співпадають з напрямами координатних осей (див. рис. 2.6). Ці вектори називаються базисними,а їх сукупність – базисом. Для кожного вектора має місце рівність

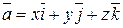, (2.4)

де - координати вектора . Формула (2.4) називається розкладанням вектора по базису.

Треба зауважити, що взаємне розташування базисних векторів може бути двох типів. Якщо, дивлячись з кінця третього вектора, ми бачимо поворот від першого до другого проти годинникової стрілки, то кажуть, що вектори утворюють праву трійку (рис. 2.7 а), в противному разі ця трійка називається лівою (рис. 2.7 б). Відповідні системи координат також називають правою та лівою.

Рис. 2. 7

Така назва пов’язана з тим, що вектори правої трійки взаємно розташовані подібно до перших трьох пальців правої руки, а вектори лівої трійки – подібно до перших трьох пальців лівої. Надалі домовимося, як це робиться здебільшого в математичній літературі, користуватися правою системою координат.

Дата добавления: 2017-02-01