Область нееквівалентних значень хвильового вектора. Зона Бріллюена

Теорема Блоха

У рівнянні Хартрі – Фока (3.23) для хвильової функції електрона в кристалі потенціальну енергію називають кристалічним потенціалом. Запишемо рівняння (3.23) у вигляді

, (6.1)

де

. (6.2)

Для дослідження властивостей розв’язків рівняння (6.1) введемо оператор трансляції [3,6]

, (6.3)

де вектор прямої решітки визначається виразом (4.1). Згідно означення (6.3) результат дії оператора трансляції на деяку функцію радіуса-вектора точки кристалу r дорівнює значенню цієї функції в точці r + l.

Подіємо оператором трансляції на ліву і праву частини рівняння (6.1). В результаті одержимо

. (6.4)

Із трансляційної симетрії нескінченно великого кристалу

, (6.5)

Враховуючи (6.2), (6.5), одержимо

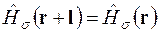. (6.6)

Підставляючи (6.6) у (6.4), маємо

. (6.7)

Із рівняння (6.7) видно, що оператори і комутують. Порівнюючи (6.1), (6.7), бачимо, що і 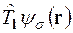є власними функціями оператора Гамільтона .

Позначимо енергію електрона в кристалі через ε_γ, де γ – набір квантових чисел, що включає і спінове квантове число σ. У загальному випадку значення енергії ε_γ є виродженим. Власними функціями гамільтоніана , що відповідають власним значенням ε_γ, є: , 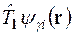та їх лінійні комбінації; i =1,2,..., n_γ; n_γ – кратність виродження енергетичного рівня ε_γ. У зв’язку з цим можна записати

. (6.8)

Для зручності ми опускаємо індекс γ біля . Візьмемо замість функцій у (6.1), (6.7) їх лінійні комбінації [5]

. (6.9)

В результаті одержимо

. (6.10)

де матриця оператора 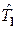у новому базисі дорівнює матриці оператора у старому базисі, тобто:

. (6.11)

Виберемо таке перетворення (6.9), щоб воно діагоналізувало матрицю . Тоді

, (6.12)

а рівняння (6.10) набуває вигляду

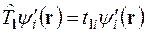, (6.13)

де , t _{l i} – власні функції і власні значення оператора трансляції .

Елементи матриці перетворення S_ji, що діагоналізує матрицю , та діагональні матричні елементи t _{l i} знаходяться із системи рівнянь

. (6.14)

Повернимось до рівняння (6.13) для власних функцій і власних значень t _{l i} оператора трансляції . З умови нормування функцій , :

, (6.15)

та рівняння (6.13) випливає

. (6.16)

Згідно означення (6.3), оператор трансляції задовольняє умові:

,

. (6.17)

Із виразу (6.17) видно, що оператори трансляції , комутують. У зв’язку з цим матриці , одним і тим же перетворенням (6.9), (6.14) можна привести до діагонального вигляду, при цьому

. (6.18)

Враховуючи (6.18), можна записати

. (6.19)

Умовам (6.16), (6.19) задовольняє

. (6.20)

Підставляючи (6.20) у (6.13), одержимо

, (6.21)

Опускаючи індекси γі біля вектора k _γі, маємо

. (6.22)

Використовуючи (6.3), із (6.22) одержимо

. (6.23)

Рівняння (6.23), що встановлює властивості хвильової функції електрона у періодичному полі кристалу, носить назву теореми Блоха.

Підставляючи (6.22) у (6.7), одержимо, що власні функції оператора трансляції (6.22) є власними функціями гамільтоніана

, (6.24)

де і = 1,2,..., n_{γ k}; n_{γ k} – кратність виродження енергетичного рівня ε_{γ k}.

Перепозначивши хвильову функцію електрона, запишемо математичний вираз теореми Блоха (6.23) у вигляді

. (7.1)

В цих означеннях рівняння для власних функцій і власних значень гамільтоніана (6.24) набуває форми

. (7.2)

Хвильова функція електрона у періодичному полі кристалу має вигляд

,

. (7.3)

Теорема Блоха формулюється саме у такій формі. Для того, щоб переконатись у правильності виразу (7.3), покажемо, що функція (7.3) задовольняє умові (7.1). Підставляючи (7.3) у (7.1), маємо

,

що і треба було довести.

Із (7.3) видно, що хвильова функція електрона у періодичному полі кристалу відрізняється від хвильової функції вільного електрона наявністю періодичного множника. Як ми побачимо далі, в наближенні ефективної маси для кристалу кубічної симетрії . В цьому випадку вектор k у виразі (7.3) є хвильовим вектором. Такий же зміст вектор k має і в загальному випадку. Простір хвильових векторів k, що зображаються на базисі оберненої решітки, називається k- простором, або оберненим простором.

Запишемо рівняння (7.1) для вектора

k´ = k + g, (7.4)

що відрізняється від хвильового вектора k на вектор вузла оберненої решітки g (5.5)

. (7.5)

Враховуючи (5.5), (4.1), маємо

, (7.6)

де N – ціле число. При цьому

. (7.7)

Підставляючи (7.7) у (7.5), одержимо

. (7.8)

Співставляючи (7.1) і (7.8) бачимо, що функції і задовольняють одному і тому ж рівнянню. З огляду на це можна записати

. (7.9)

Записуючи рівняння (7.2) для вектора k´, маємо

. (7.10)

Співставляючи (7.2), (7.10) і враховуючи (7.9), в результаті одержимо

. (7.11)

Враховуючи (7.9), (7.11), можна зробити висновок, що розв’язки рівняння Шредінгера (7.2) для векторів k і k´ співпадають. У зв’язку з цим вектори k і k´, що пов’язані співвідношенням (7.4), є еквівалентними. Підставляючи (7.4) у (7.9), (7.11), одержимо

, (7.12)

.

На основі виразів (7.12) можна стверджувати, що хвильова функція і енергія електрона в кристалі є періодичними функціями в оберненому просторі.

Із (7.4) випливає, що нееквівалентні вектори k знаходяться тільки в одній із основних комірок оберненої решітки. Зазвичай у якості області нееквівалентних значень хвильового вектора k вибирають першу зону Бріллюена, чи просто зону Бріллюена.

Зона Бріллюена являє собою об’єм оберненої решітки, що обмежений площинами, які ділять навпіл і перпендикулярні до відрізків, що з’єднують один вузол оберненої решітки з усіма сусідніми вузлами. При цьому об’єм зони Бріллюена є рівновеликий до об’єму основної комірки оберненої решітки.

Зона Бріллюена двовимірної решітки зображена на рис.3 (заштрихована область). Такий вибір області нееквівалентних значень хвильового вектора k має перевагу перед іншими ту, що зона Бріллюена ясно відображає властивості симетрії кристалу.

Рис.7.1. Зона Бріллюена двовимірної решітки.

Об’єм зони Бріллюена згідно означення і (5.8) дорівнює

. (7.13)

Дата добавления: 2017-02-01