Наближення майже вільних (слабо зв’язаних) електронів

Функції Ван’є

Теорема Ван’є

Енергія електрона в ідеальному кристалі (7.12) є періодичною функцією в оберненому просторі. Як вже зазначалося, функцію, періодичну в просторі оберненої решітки, можна розкласти в ряд Фур’є (9.13) за векторами вузлів прямої решітки. Зважаючи на це, запишемо

(11.1)

Побудуємо оператор заміною у виразі (11.1) вектора на оператор . В результаті маємо

(11.2)

Знайдемо результат дії оператора на хвильову функцію Блоха (7.3). Використовуючи (11.2), можна записати

(11.3)

Розкладаючи у виразі (11.3) експоненту в ряд, одержимо

(11.4)

Одержаний ряд можна розглядати як ряд Тейлора за степенями

Тут введено позначення: , , , , , . Підставляючи (11.4) в (11.3), одержимо

(11.5)

Скориставшись у (11.5) теоремою Блоха (7.1), маємо

(11.6)

Підставляючи (11.1) у (11.6), в результаті одержимо:

(11.7)

Співвідношення (11.7) називається теоремою Ван’є.

Функції Блоха (7.12) періодичні в - просторі з періодами, що дорівнюють векторам 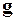вузлів оберненої решітки. Це означає, що можна розкласти в ряд Фур’є (9.13) за векторами - вузлів прямої решітки. Таким чином, існує ряд Фур’є

, (12.1)

коефіцієнти якого

(12.2)

Функції , що є зображенням Фур’є для функції Блоха , називаються функціями Ван’є. Функції Блоха є власними функціями гамільтоніана для електрона кристалу (див. (7.2)), тому їх можна вважати ортонормованими.

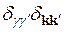(12.3)

Покажемо, що функції Ван’є також є ортонормованими. Для цього запишемо

= (12.4)

Підставляючи (12.2) у (12.4), маємо:

= (12.5)

Використовуючи умову ортонормованості (12.3) функцій Блоха, надамо виразу (12.5) вигляду

= = . (12.6)

Можна показати, аналогічно (9.14), що

(12.7)

Підставляючи (12.7) у (12.6), в результаті одержимо

= (12.8)

Таким чином, функції Ван’є взаємно ортогональні як за номером енергетичної зони , так і за номером вузла l.

Отже, крім ортонормованого базису функцій Блоха, ми маємо ортонормований базис функцій Ван’є. Підставляючи (7.3) у (12.2), одержимо

=

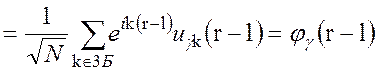(12.9)

Таким чином, функції Ван’є для всіх вузлів кристалічної решітки при фіксованому номері енергетичної зони мають один і той же вигляд, але центровані на різних вузлах.

На відміну від функцій Блоха, що є власними функціями гамільтоніана, функції Ван’є у загальному випадку не є власними функціями гамільтоніана, а є лише їх лінійними комбінаціями (12.2).

Другою суттєвою відмінністю функцій Ван’є від функцій Блоха є те, що кожна з функцій Ван’є локалізована поблизу свого вузла . Покажемо це в наближенні ефективної маси для кристалів кубічної симетрії. У цьому наближенні, як побачимо далі, періодичний множник Блоха (7.3). Враховуючи зазначене, запишемо функцію Ван’є (12.2) у вигляді

= (12.10)

Розраховуючи суму у (12.10) аналогічно (9.14) в результаті одержимо

= , (12.11)

де - об’єм примітивної комірки прямої решітки. Вираз (12.11) записано для , і= 1,2,3.

Вираз (12.11) має максимальне значення при , i=1,2,3; при збільшенні він швидко зменшується, осцилюючи. Таким чином, функція Ван’є = має максимум в точці , швидко спадаючи при зростанні . Аналогічний доказ можна зробити і у більш загальному випадку – для кристалу довільної структури і для загального вигляду функції Блоха (7.3) (слід тільки вважати, що слабо залежить від ).

Як буде видно надалі, завдяки зазначеній властивості локалізації базис функцій Ван’є має перевагу над базисом функцій Блоха при описі електронних станів кристалу зі значною кількістю домішок.
РОЗДІЛ 2. МЕТОДИ РОЗРАХУНКУ ОДНОЕЛЕКТРОННИХ СТАНІВ КРИСТАЛУ

Нехай у рівнянні Шредінгера (6.1), що визначає одноелектронні стани кристалу, кристалічний потенціал в середньому є значно менший від кінетичної енергії електрона. Це означає, що електрони в таких станах слабо зв’язані з атомами і майже вільно рухаються по кристалу.

У цьому випадку за гамільтоніан нульового наближення в рівнянні (10.40) можна вибрати оператор кінетичної енергії , а гамільтоніаном збурення вважати оператор потенціальної енергії Рівняння (10.40) у цьому випадку набуває вигляду

, (13.1)

де

. (13.2)

Розв’язком рівняння (13.1) є

,

(13.3)

Співставляючи рівняння (10.40) і (13.1), бачимо, що індексом стану в цьому випадку є хвильовий вектор . У зв’язку з цим замінимо в рівнянні (10.43) індекс l на 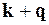, а індекс m на , врахувавши, що . Тут індексом ми позначимо стани електрона при відсутності збурення. В результаті рівняння (10.43) набуває вигляду

- . (13.4)

Власна функція гамільтоніана електрона в кристалі (6.2), що відповідає власному значенню , дорівнює (10.45)

. (13.5)

Встановимо зв'язок між зображеннями Фур’є 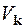і матричними елементами потенціальної енергії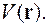

Використовуючи (10.18), (13.3), (9.2) запишемо

=

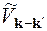= . (13.6)

Підставляючи (13.6) у (13.4), одержимо

. (13.7)

Після заміни рівняння (13.7) набуває вигляду:

. (13.8)

Член суми в рівнянні (13.8), що відповідає , містить 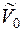. Коефіцієнт ряду Фур’є 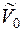(13.6) дорівнює середньому значенню потенціальної енергії

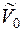= (13.9)

і може мати значну величину. Змінивши відповідним чином початок відліку потенціальної енергії , можна вважати, що коефіцієнти ряду Фур’є для потенціальної енергії у наближенні майже вільних електронів є малими і задовольняють умові

. (13.10)

Знайдемо розв’язок системи рівнянь (13.8) методом розкладу за степенями малого параметру . Для цього запишемо

(13.11)

.

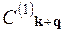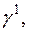
Тут величини , , ,... пропорційні відповідно і т. д. Аналогічно означені члени ряду для .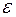

Зважаючи, що при відсутності збурення електрон знаходиться в стані, який описується хвильовою функцією (13.3), можна покласти

= . (13.12)

У цьому можна легко переконатися, використовуючи (13.5).

Підставимо (13.11) у (13.8) і прирівняємо члени одного порядку малості. Члени нульового порядку малості задовольняють рівнянню

. (13.13)

Враховуючи (13.12), з рівняння (13.13) знаходимо

. (13.14)

У першому порядку малості маємо

, (13.15)

Тут перше рівняння одержано з (13.8) при , а друге – при

Використовуючи (13.12), (13.14), з рівнянь (13.15) знаходимо

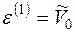, (13.16)

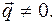= , (13.17)

Коефіцієнт знаходимо з умови нормування хвильової функції (13.5), яка повинна виконуватись з точністю до членів першого порядку включно. В результаті маємо

= 0. (13.18)

У другому порядку малості з рівняння (13.8) при одержимо

. (13.19)

Підставляючи (13.12), (13.17) у (13.19), знаходимо

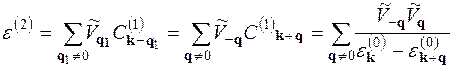. (13.20)

Підставляючи (13.14), (13.16), (13.20) у другу рівність (13.11), одержимо вираз для енергії електрона

. (13.21)

Тут ми скористались співвідношенням

, (13.22)

що випливає з умови дійсності потенціальної енергії

. (13.23)

Із виразів (13.5), (13.11), (13.12), (13.17) одержимо для хвильової функції електрона

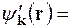
. (13.24)

Скориставшись (13.6), запишемо вирази (13.21), (13.24) у вигляді

(13.25)

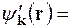
. (13.26)

Розглянемо ідеальний кристал. У цьому випадку потенціальна енергія задовольняє умову

. (13.27)

Згідно (9.10), таку періодичну функцію можна розкласти в ряд Фур’є за векторами оберненої решітки, тобто записати у вигляді

. (13.28)

Підставляючи (13.28) у (13.6), можна показати, що

. (13.29)

За умови (13.29) система рівнянь (13.8) зводиться до

, (13.30)

при цьому , якщо .

Вираз (13.5) для хвильової функції електрона у цьому випадку набуває вигляду

. (13.31)

Співставляючи (13.8) і (13.30), а також (13.5) і (13.31), бачимо, що рівняння (13.30) і вираз (13.31) одержуються відповідно з рівняння (13.8) і виразу (13.5) заміною на .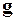

Отже, розв’язок рівняння (13.30) одержується з виразу (13.21) заміною на 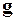і має вигляд

. (13.32)

Хвильова функція електрона дорівнює (див. (13.24))

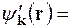
. (13.33)

Якщо хвильовий вектор задовольняє для деякого вектора 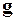умову

, (13.34)

то відповідний член суми у (13.32) і (13.33) прямує до нескінченності. Це означає, що розв’язок системи рівнянь (13.30) у вигляді (13.32), (13.33) не існує. Використовуючи (13.3), запишемо умову (13.34) у вигляді

. (13.35)

Хвильовий вектор задовольняє умову (13.35), якщо кінець вектора лежить на площині, що обмежує зону Бріллюена (рис. 13.1)

Рис.13.1. Положення хвильового вектора в зоні Бріллюена, яке відповідає умові (13.35).

Рівняння (13.35) є рівнянням площини, яка обмежує зону Бріллюена.

Рівність (13.34) є умовою виродження власних значень гамільтоніана (13.2) нульового наближення. Таким чином, розв’язок системи рівнянь (13.30) можна шукати за методом теорії збурень для випадку вироджених власних значень гамільтоніана нульового наближення. У цьому випадку хвильову функцію електрона можна записати у вигляді лінійної комбінації власних функцій , 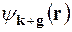гамільтоніана нульового наближення, що відповідають одному і тому ж власному значенню (13.3). Отже, хвильова функція електрона записується у вигляді (див. (13.31))

. (13.36)

Такий же вигляд має хвильова функція і в більш загальному випадку, коли рівність (13.34) виконується наближено. Рівняння для коефіцієнтів , хвильової функції (13.36) можна одержати із системи рівнянь (13.30), якщо в ній зберегти тільки ті члени, що містять , , тобто записати у вигляді

– (13.37)

.

Умовою існування розв’язку системи рівнянь (13.37) є

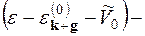
. (13.38)

При одержанні виразу (13.38) ми використали умову дійсності потенціальної енергії (13.22). Рівняння (13.38) для енергії електрона 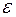має два корені

. (13.39)

Для випадку, коли умова (13.34) виконується точно, корені рівняння (13.38) мають вигляд

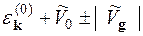= . (13.40)

Таким чином, двократно вироджений рівень енергії розщепився на два рівні , (13.40).

Графік залежностей енергії електрона 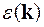від хвильового вектора для одновимірної решітки зображено на рис.9.

Для першої зони Бріллюена проекція хвильового вектора приймає значення , де a – період кристалічної решітки. При значеннях , далеких від , де n = 1,2,3 … - ціле число, поправка до енергії мала, тобто можна вважати (13.32). При 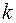= енергія електрона у кристалі 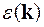суттєво відрізняється від енергії вільного електрона : рівень енергії розщеплюється на величину 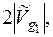і т. д. (13.40). У спектрі енергії електрона виникають заборонені інтервали енергії шириною і т.д. Енергетичний спектр електрона набуває зонного характеру, тобто дозволені інтервали енергії чергуються із забороненими. Як видно із одержаних результатів, у випадку майже вільних електронів їх енергетичний спектр має майже параболічний характер (13.3). У відповідності з умовою (7.12) енергія електрона в межах кожної дозволеної зони є періодичною функцією хвильового вектора (зображена тонкими лініями, що продовжують вліво і вправо відрізки параболи на рис.9). Це дозволяє розглядати всі енергетичні зони в межах першої чи приведеної зони Бріллюена. Такий підхід до опису енергетичного спектру називається методом приведених зон.

Рис.13.2. Енергетичний спектр слабо зв’язаних електронів.

Підхід, у якому значення хвильового вектора не обмежуються першою зоною Бріллюена, називається методом розширених зон (залежність енергії від хвильового вектора зображена на рис.13.2 жирними лініями). Ми бачимо, що для слабо зв’язаних електронів у першій зоні Бріллюена енергія електрона в послідовних енергетичних зонах при k = 0 позмінно приймає мінімальне і максимальне значення. Однією з характерних особливостей одновимірного випадку, що показаний на рис.13.2, є те, що послідовні зони дозволеної енергії електрона завжди розділені забороненими інтервалами енергії. У двовимірному і тривимірному випадках це не завжди має місце. В цих випадках енергія електрона в деякій точці зони Бріллюена для верхньої енергетичної зони може бути нижчою від енергії, взагалі кажучи, в іншій точці зони Бріллюена для нижньої енергетичної зони. У цьому випадку має місце перекриття енергетичних зон. Внаслідок цього може заповнюватись електронами верхня енергетична зона при неповністю заповненій нижній зоні.

Дата добавления: 2017-02-01