Наближення ефективної маси

Якщо енергія в точці має мінімум чи максимум, то її можна розкласти в ряд Тейлора

=

= (16.1)

де проекції вектора на вісі декартової системи координат. У виразі (16.1) ми врахували, що в точці екстремуму =0, і обмежимось розкладом до квадратичних членів. Переносячи початок відліку енергії і хвильового вектора в точку екстремуму і враховуючи, що в новій системі відліку =0, , одержимо

. (16.2)

З метою наближення опису руху електрона в періодичному полі кристалу до опису руху вільного електрона введемо тензор оберненої ефективної маси.

. (16.3)

Підставляючи (16.3) у (16.2), маємо

. (16.4)

Діагоналізуючи квадратичну форму (16.4), маємо (див. § 10)

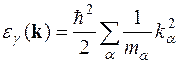, (16.5)

де

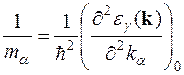, . (16.6)

Можна дослідити компоненти тензора оберненої ефективної маси у виразі (16.4), використовуючи також умови симетрії кристалу. Нехай R є перетворення прямої кристалічної решітки, при якому атоми кожного сорту переходять у положення інших атомів того ж сорту.

При такому перетворенні енергія електрона в кристалі не змінюється, тобто

. (16.7)

Для кристалів кубічної симетрії всі три компоненти тензора оберненої ефективної маси 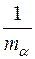однакові, тому можна записати

. (16.8)

Енергія електрона в цьому випадку дорівнює

, (16.9)

тобто дорівнює енергії електрона з масою .

Зазначимо, що компоненти тензора оберненої ефективної маси мають розмірність (маса) . Біля нижнього краю зони, де має мінімум (див. (14.19)), ефективна маса (16.6) додатня (). Поблизу максимума ефективна маса від’ємна ( <0).

Як вже зазначалось, при розкладі енергії електрона (16.1) в ряд Тейлора за степенями проекцій хвильового вектора ми обмежились квадратичними членами. Таке наближення називається наближенням ефективної маси.

В наближенні ефективної маси рівняння (15.26) для хвильової функції електрона в полі домішки набуває простого вигляду

. (16.10)

Для кристалів кубічної симетрії рівняння (16.10) має більш просту форму

. (16.11)

Для ідеального кристалу і рівняння (16.11) має особливо простий вигляд

. (16.12)

Роз’вязком рівняння (16.12) є

, . (16.13)

Зважаючи нате, що (16.13) є функцією Блоха (7.3), одержуємо, що в наближенні ефективної маси для кристалів кубічної симетрії періодичний множник Блоха

. (16.14)

Таким чином, у наближенні ефективної маси стани електрона в кристалі кубічної симетрії подібні до станів вільного електрона з ефективною масою .

Дата добавления: 2017-02-01