Електронна теплоємність

Електронна теплоємність при постійному об’ємі кристалу дається виразом

. (20.1)

Похідна за температурою від середньої повної електронної енергії кристалу (19.3) береться за умови постійного числа електронів. Ця умова буде виконуватись автоматично, якщо у виразі (19.3) для середньої повної електронної енергії енергію електрона відраховувати від рівня Фермі m. Тоді вираз для електронної теплоємності можна подати у вигляді

, (20.2)

де повна електронна енергія дорівнює

. (20.3)

Підставляючи (19.5) у (20.3), маємо

(20.4)

Знаючи густину електронних станів , за формулами (20.2), (20.4) можна розрахувати електронну теплоємність.

Для довільної температури T розрахунок електронної теплоємності виконується числовими методами. Але для низьких температур існує аналітичний метод розрахунку інтегралу за енергією від довільної функції, помноженої на функцію Фермі.

Застосуємо цей метод для аналітичного розрахунку інтегралу (20.4). Будемо відраховувати рівень Фермі m від дна енергетичної зони, нижче якого всі енергетичні рівні є зайнятими. В новій шкалі енергії рівень Фермі називається енергією Фермі і позначається як e_F. Опускаючи незалежну від температури складову, перепишемо вираз (20.4) у вигляді

. (20.5)

Введемо для зручності позначення

. (20.6)

Підставляючи (20.6) в (20.5), матимемо

. (20.7)

Інтегруючи у виразі (20.7) по частинам, одержимо

, (20.8)

де

. (20.9)

Враховуючи, що на нижній межі інтегрування , а на верхній межі дорівнюють нулю, перша складова у виразі (20.8) зникає. В результаті одержимо

. (20.10)

Легко показати, що

. (20.11)

Крім того легко бачити, що

. (20.12)

З виразів (20.11), (20.12) випливає

, (20.13)

де – d - функція Дірака.

Таким чином, множник під знаком інтегралу (20.10) при низьких температурах

(20.14)

є різкою функцією енергії з максимальним значенням в точці 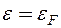. У зв’язку з цим розкладемо функцію у вираз (20.10) в ряд Тейлора поблизу точки 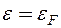. Вводячи безрозмірну енергію

, (20.15)

маємо

(20.16)

Підставляючи (20.16) в (20.10), матимемо

. (20.17)

Враховуючи, що підінтегральна функція у виразі (20.17) є різкою функцією енергії h в околі точки h =0, та умову (20.14), нижню межу інтегрування покладено рівною ¥. При одержанні виразу (20.17) враховано також, що інтеграл в межах (-¥,¥) від непарної функції дорівнює нулю. У зв’язку з цим друга складова у правій частині формули (20.16) не дає внеску в інтеграл.

Розкладаючи підінтегральну функцію у виразі (20.17) в ряд Тейлора за степенями , маємо

(20.18)

Після інтегрування по частинам у виразі (20.18), одержимо

. (20.19)

Ряд у правій частині виразу (20.19) можна підсумувати, скориставшись рядом Фур’є для функції x ² в інтервалі :

. (20.20)

Скориставшись виразом (20.20) при x =0, для інтегралу (20.19) матимемо

. (20.21)

Підставляючи (20.21) в (20.17), в результаті одержимо

. (20.22)

При одержанні виразу (20.22) використано (20.15), (20.16). Враховуючи (20.6), (20.9), одержимо

,

. (20.23)

З виразу (20.23) маємо

. (20.24)

Підставляючи (20.6), (20.9), (20.24) в (20.22), в результаті для повної електронної енергії кристалу при низьких температурах маємо

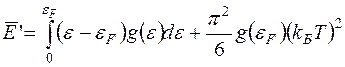. (20.25)

Використовуючи (20.2), (20.25) для електронної теплоємності кристалу при низьких температурах одержимо

. (20.26)

Таким чином, електронна теплоємність при низьких температурах пропорційна першій степені температури. Коефіцієнт пропорційності визначається густиною електронних станів на рівні Фермі. Вираз (20.26) є справедливим як для ідеальних, так і реальних кристалів. Формула (20.26) дозволяє з експериментальних даних для електронної теплоємності при низьких температурах визначити густину електронних станів на рівні Фермі. Розрахунки електронних станів на рівні Фермі в певних моделях кристалу та порівняння теоретичних результатів з експериментальними даними дає можливість робити висновки про адекватність тих чи інших моделей для опису твердих тіл.

Дата добавления: 2017-02-01