Коливання ідеальної кристалічної решітки

Для ідеальної кристалічної решітки номер вузла кристалічної решітки в системі рівнянь (21.10) приймає нескінченне число значень. У зв’язку з цим коливання кристалічної решітки описується системою нескінченного числа рівнянь (21.10). Використовуючи властивості трансляційної симетрії ідеального кристалу, систему нескінченного числа рівнянь (21.10) можна звести до системи кінцевого числа рівнянь. Для цього будемо шукати розв’язок системи рівнянь (21.10) у вигляді

. (22.1)

Підставляючи (22.1) в (21.10), після нескладних перетворень одержимо систему 3 r рівнянь для невідомих величин e_a (i) (a = x, y, z; i = 0,1,…, r -1):

, (22.2)

де

(22.3)

є елементами так званої динамічної матриці кристалу. З властивості трансляційної симетрії кристалу випливає, що залежність матриці силових постійних від і зводиться до її залежності від різниці цих векторів . У зв’язку з цим після підсумовування по n¢ у (22.3) права частина цього рівняння не залежить від n. Без умови трансляційної симетрії кристалу розв’язку (22.10) у вигляді (22.1) не існувало б, оскільки ліва частина (22.2) залежала б від n, а права — ні.

Легко переконатись, що динамічна матриця (22.3) є самоспряженою, тобто задовольняє умові

. (22.4)

Зауважимо, що матриця в рівнянні руху кристалічної решітки (22.2) виявилась самоспряженою завдяки виділення окремо множника у виразі (22.1).

Перепишемо рівняння (22.2) у вигляді

. (22.5)

Умовою розв’язку системи лінійних однорідних рівнянь (22.5) є рівність нулю детермінанта матриці:

. (22.6)

Рівняння (22.6) є алгебраїчним рівнянням степені 3 r відносно w ². Воно має 3 r розв’язків, які залежать від хвильового вектора k, оскільки від вектора k залежить динамічна матриця . Будемо враховувати тільки додатні значення w. Від’ємні значення w врахуються, коли будемо будувати загальний розв’язок системи рівнянь (21.10) шляхом лінійної комбінації часткових розв’язків (22.1), що записані в комплексній формі. При цьому необхідно врахувати, що розв’язки системи (21.10) є дійсними.

Позначимо ці розв’язки рівняння (22.6) у вигляді w_j (k), де j пробігає значення j =0,1,…,3 r.

Підставляючи розв’язки w_j (k) у систему рівнянь (22.2), одержимо для кожного з них набір векторів поляризації зміщень атомів , що задовольняють системі рівнянь

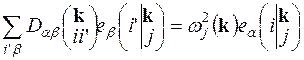, (22.7)

де a = x, y, z; i =0,1,…, r -1.

Дата добавления: 2017-02-01