Нормальні координати кристалічної решітки

Потенціальна енергія кристалу (21.3) є квадратичною формою зміщень атомів з положення рівноваги . Враховуючи, що динамічна матриця є самоспряженою (див. (22.4)), квадратичну форму для потенціальної енергії можна привести до діагонального вигляду. Це здійснюється шляхом розкладу величин в ряд Фур’є по плоским хвилям і розкладу коефіцієнтів ряду Фур’є по власним векторам динамічної матриці :

. (25.1)

Використовуючи умову дійсності

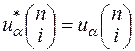(25.2)

і співвідношення (23.6), одержимо

. (25.3)

Підставляючи (25.1), (22.3) у (21.3), використовуючи рівняння динаміки кристалічної решітки (22.7), умови ортонормованості (9.3), (23.1) та умову дійсності, матимемо

. (25.4)

Кінетична енергія кристалу дорівнює

. (25.5)

Виконуючи для квадратичної форми, що відповідає кінетичній енергії (25.5), перетворення, аналогічні описаним вище, одержимо

. (25.6)

Функція Лагранжа кристалу дорівнює

. (25.7)

Величини і є відповідно узагальненими координатами і узагальненими швидкостями кристалічної решітки. Узагальнений імпульс, канонічно спряжений до координати , є

. (25.8)

Узагальнені координати є комплексними . Тут для зручності введено узагальнений імпульс , що канонічно спряжений до комплексно спряженої узагальненої координати .

Із (25.3), (25.8) випливає

. (25.9)

Функція Гамільтона решітки має вигляд

. (25.10)

Перейдемо до дійсних узагальнених координат шляхом перетворення

. (25.11)

Використовуючи (25.7), (25.11), виразимо функцію Лагранжа через дійсні узагальнені координати і швидкості:

. (25.12)

Узагальнений імпульс, канонічно спряжений до узагальненої координати , є

. (25.13)

Функція Гамільтона, виражена через дійсні узагальнені координати і імпульси, дорівнює

. (25.14)

Величина (25.14) є функцією Гамільтона системи гармонічних незалежних осциляторів. У зв’язку з цим узагальнені координати називаються ще нормальними координатами кристалічної решітки.

Дата добавления: 2017-02-01