Взаємодія електронів з коливаннями кристалічної решітки

Вийдемо тепер за рамки адіабатичного наближення (§1), вважаючи, що ядра атомів кристалу рухаються настільки швидко, що електрони не встигають підлаштуватись до їх нових положень. В цьому випадку вектори зміщень атомів з положень рівноваги (21.2) в гамільтоніані системи не є параметрами, а є операторами її динамічних змінних. Атоми, що вийшли з положень рівноваги в процесі коливань кристалічної решітки, порушують умову трансляційної інваріантності кристалу. Це призводить до розсіяння електронів на коливаннях кристалічної решітки.

В наближенні, коли нехтується взаємодія електронів з коливаннями кристалічної решітки, енергія електрона в одноелектронному наближенні визначається рівнянням (7.2). Знайдемо поправку до енергії електрона, зумовлену його взаємодією з коливаннями решітки.

Наближення потенціалу деформації.

Коливання кристалічної решітки викликає локальну деформацію кристалу, яку ми будемо описувати тензором деформації

, (27.1)

де x_a – проекція радіуса-вектора r точки кристалу на вісь a декартової системи координат, u_a – a – проекція вектора зміщення атома з положення рівноваги (21.2).

Враховуючи взаємодію електрона з коливаннями кристалічної решітки, енергію електрона, яка є скаляром, можна подати у вигляді

, (27.2)

де C_ab, C' – сталі, що не залежать від деформації кристалу. Підсумовування по подвійним індексам у виразі (27.2) і надалі для простоти запису опускається.

Розглядаючи примітивну комірку, із означення тензора деформації u_ab (27.1) легко показати, що сума його діагональних компонентів дорівнює відносній зміні об’єму примітивної комірки , тобто

. (27.3)

Для кристалів із сферичною поверхнею Фермі енергія електрона e (27.2) у довгохвильовому наближенні () залежить від компонентів тензора деформації u_ab тільки через відносну зміну об’єму кристалу D. В цьому випадку у виразі (27.2) C_ab = C ₁ d_ab. Враховуючи зазначене та (27.3), запишемо вираз (27.2) для енергії електрона у вигляді

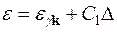, (27.4)

де

є сталою, яку можна визначити з результатів вимірювання залежності енергетичних характеристик кристалу від деформації.

Енергія електрона e (27.4) є власним значенням деякого гамільтоніану

, (27.5)

де – гамільтоніан електрона в ідеальному кристалі (див. (6.2), (7.2)), – так званий оператор розширення, що визначається з відносної зміни об’єму кристалу D (27.3) згідно правил переходу від класичної до квантової механіки.

Підставляючи (25.1), (27.1) у (27.3), одержимо

. (27.6)

При одержанні виразу (27.6) вважалось, що відносна зміна об’єму кристалу D не залежить від його об’єму, який покладено рівним W=1. Тут для простоти вважалось, що кристал складається із атомів одного сорту і введено величину r = NM, що є густиною маси. У такому запису вираз (27.6) можна узагальнити на кристали з довільним числом сортів атомів, підсумовуючи у (27.6) лише по акустичним гілкам коливань j =1,2,3. У формулі (27.6) покладено, що радіус-вектор вузла кристалічної решітки є рівним радіусу-вектору електрона r, тобто 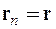. На відміну від хвильового вектора електрона k, хвильовий вектор коливань кристалічної решітки у (27.6) позначено через q.

Переходячи у формулі (27.6) від узагальненої координати до оператора координати і використовуючи вираз (26.22), в результаті для оператора розширення одержимо

.

(27.7)

Враховуючи умову (23.5), вираз (27.7) для оператора розширення можна подати у вигляді

.

(27.8)

У довгохвильовому наближенні можна покласти, що в кристалі існують чисто повздовжні (j =1) і чисто поперечні (j =2,3) коливання. Враховуючи зазначене, в результаті матимемо

. (27.9)

Із виразу (27.9) видно, що в наближенні потенціалу деформації електрони взаємодіють лише з повздовжніми коливаннями кристалічної решітки.

Дата добавления: 2017-02-01