Теплоємність кристалічної решітки

Для розрахунку теплоємності запишемо середнє значення енергії коливань кристалічної решітки (26.6)

, (29.1)

де – функція Бозе – Ейнштейна

. (29.2)

Підставляючи (29.2) у (29.1), маємо

, (29.3)

де незалежна від температури величина

. (29.4)

Вводячи функцію розподілу частот коливань кристалічної решітки (густину фононних станів), вираз (29.3) можна подати у вигляді

, (29.5)

де – функція розподілу частот коливань кристалічної решітки, що визначається аналогічно густині електронних станів (19.19),

. (29.6)

Модель Дебая та модель Ейнштейна.

Виконаємо розрахунок теплоємності кристалічної решітки в моделі Дебая для спектру частот акустичних коливань та в моделі Ейнштейна для спектру частот оптичних коливань. Для цього розіб’ємо суму у правій частині (29.3) на суму по акустичним гілкам коливань і суму по оптичним гілкам коливань. В результаті матимемо

. (29.7)

Енергія акустичних коливань

, (29.8)

де функція розподілу частот акустичних коливань

. (29.9)

Енергія оптичних коливань

. (29.10)

В моделі Дебая частота акустичних коливань покладається рівною (див. (23.16))

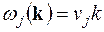, j =1,2,3. (29.11)

Враховуючи (29.11), розраховуємо величину у виразі (29.9), яка дорівнює

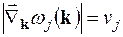. (29.12)

Використовуючи (29.12), нескладно одержати

. (29.13)

Введемо ефективну швидкість акустичних хвиль v ₀ згідно формули

, (29.14)

де і 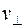– швидкості повздовжніх і поперечних акустичних хвиль відповідно.

Підставляючи (29.14) у (29.13), одержимо

. (29.15)

Інколи буває зручним виразити сталу у правій частині (29.15) через максимальну частоту w_m акустичних коливань згідно формули

. (29.16)

Підставляючи (29.15) у (29.16), матимемо

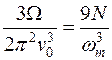. (29.17)

Враховуючи (29.17), із (29.15) одержимо

. (29.18)

Підставляючи (29.18) у (29.8), для енергії акустичних коливань матимемо

. (29.19)

Вводячи безрозмірну змінну та температуру Дебая , запишемо вираз (29.19) для енергії акустичних коливань у вигляді

. (29.20)

Введемо тепер функцію Дебая

. (29.21)

Підставляючи (29.21) у (29.20), в результаті для енергії акустичних коливань одержимо

. (29.22)

Перейдемо тепер до розрахунку оптичних коливань. Використаємо для цього модель Ейнштейна для спектру частот оптичних коливань, згідно якої

, j =4,5,…,3 r. (29.23)

Враховуючи (29.23) і вводячи температури Ейнштейна , запишемо енергію оптичних коливань (29.10) у вигляді

. (29.24)

Підставляючи (29.22), (29.24) у (29.7), в результаті для енергії коливань кристалічної решітки одержимо

. (29.25)

Дослідимо вираз (29.25) при високих температурах . Враховуючи, що в цьому випадку верхня межа інтегрування у виразі (29.21) для прямує до нуля, і розкладаючи під знаком інтеграла функцію в ряд 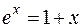, одержимо

. (29.26)

Аналогічно одержимо

. (29.27)

Підставляючи (29.26), (29.27) у (29.25), матимемо

. (29.28)

Теплоємність кристалічної решітки при постійному об’ємі визначається виразом

. (29.29)

Використовуючи (29.28), із (29.29) для теплоємності кристалічної решітки при високих температурах одержимо

. (29.30)

Теплоємність одного моля речовини згідно (29.30) дорівнює

. (29.31)

Із виразу (29.30) видно, що теплоємність кристалічної решітки при високих температурах не залежить від температури, що знаходиться у відповідності з законом Дюлонга – Пті.

Розглянемо тепер теплоємність при низьких температурах . Враховуючи, що в цьому випадку верхня межа інтегрування у виразі (29.21) для 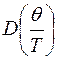прямує до нескінченності, одержимо

. (29.32)

Враховуючи, що сума по оптичним гілкам коливань у правій частині рівності (29.25) при низьких температурах прямує до нуля за експоненційним законом, нехтуємо цією сумою в порівнянні з величиною . Це означає, що основний внесок в енергію коливань кристалічної решітки при низьких температурах дають акустичні коливання, а ймовірність збудження оптичних коливань є незначною. В результаті для енергії коливань кристалічної решітки при низьких температурах одержимо

. (29.33)

Підставляючи (29.33) у (29.29), для теплоємності кристалічної решітки матимемо

. (29.34)

Із (29.34) видно, що теплоємність кристалічної решітки при низьких температурах описується законом Дебая .

При довільних температурах теплоємність розраховується за формулами (29.25), (29.29).

Дата добавления: 2017-02-01