Рівняння руху кристалічної решітки

РОЗДІЛ 3. ТЕОРІЯ КОЛИВАНЬ КРИСТАЛІЧНОЇ РЕШІТКИ

В адіабатичному наближенні (§1) розв’язок рівняння Шредінгера для кристалу зводиться до розв’язку рівняння (1.7), що описує рух електронів в полі нерухомих ядер та до розв’язку рівняння (1.12), що описує рух ядер. При цьому потенціальною енергією в рівнянні руху ядер (1.12) є власні значення енергії рівняння руху електронів (1.7), розв’язок якого розглянуто в попередніх розділах 1.2. Таким чином, будемо вважати, що нам відомо потенціальна енергія кристалічної решітки. Рівняння руху кожного атома кристалу описується силою, що складається із зовнішньої сили, в полі якої знаходиться кристал, і потенціальної сили з боку інших атомів кристалу, яка виражається через його потенціальну енергію. Для запису рівняння руху введемо координати кристалічної решітки. Рівноважне положення атомів у вузлах кристалічної решітки описується вектором

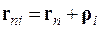, (21.1)

де – радіус-вектор вузла кристалічної решітки з номером n (4.1), – вектор, що описує положення атома сорту i в примітивній комірці кристалу. Номер сорту атома i приймає значення , де – число сортів атомів в кристалі.

Вектор зміщення атома сорту i в примітивній комірці n позначимо, як . Таким чином, положення атома сорту i в примітивній комірці n в довільний момент часу можна описати вектором

. (21.2)

Вектор зміщення атома у виразі (21.2) залежить від положення атома і часу. Ця залежність визначається рівнянням руху кристалічної решітки.

Для запису рівняння руху кристалічної решітки розглянемо потенціальну енергію кристалу F. Потенціальна енергія кристалу Fє функцією миттєвих положень всіх атомів. Розкладаючи функцію F в ряд Тейлора за степенями проекцій векторів зміщень атомів на вісі декартової системи координат, отримаємо

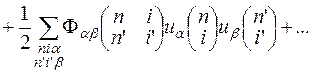. (21.3)

В рамках гармонічного наближення знехтуємо у виразі (21.3) всіма степенями вище другої. Тут F₀ є потенціальною енергією атомів кристалу в положенні рівноваги. У виразі (21.3)

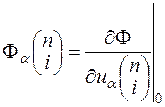, (21.4)

, (21.5)

де індекс 0 означає, що похідна береться для рівноважного положення атомів.

Сила, що діє на атом сорту i в примітивній комірці n з боку інших атомів і зовнішнього потенціального поля, визначається потенціальною енергією кристалу згідно виразу

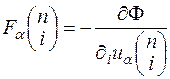. (21.6)

Підставляючи (21.3) в (21.6), отримаємо

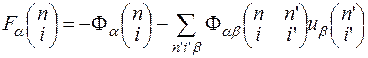. (21.7)

Величини , , що визначають потенціальну енергію кристалу та сили, що діють на атоми кристалу, називають силовими постійними. Величина ще має назву матриці силових постійних.

Згідно (21.7) , має зміст взятої з оберненим знаком a – проекції сили, яка діє в рівноважній конфігурації на атом в положенні . Для вільного кристалу, що не знаходиться в зовнішньому полі, ця сила дорівнює нулю. Таким чином, для цього випадку маємо

. (21.8)

Рівняння руху кристалічної решітки можна подати у вигляді

, (21.9)

де M_i – маса атома сорту i. Підставляючи (21.7) і (21.8) у (21.9), отримаємо систему рівнянь

. (21.10)

Система рівнянь (21.10) описує рух кристалічної решітки вільного кристалу.

Змістимо всі атоми кристалу на довільний постійний вектор

. (21.11)

Підставляючи (21.11) в (21.10), матимемо

. (21.12)

Враховуючи, що компоненти вектора a_b є незалежними, з (21.12) одержимо

. (21.13)

Дата добавления: 2017-02-01