Рух електрона в кристалі, що знаходиться в зовнішньому полі

Нехай кристал знаходиться в зовнішньому полі. Тоді крім періодичного поля решітки на електрон діє зовнішня сила F. Вважатимемо, що ця сила є малою і задовольняє умові F a<< , де a – стала решітки, - ширина забороненої зони. В цьому випадку така сила не приводить до переходу електрону в інші енергетичні зони. Дія цієї сили на електрон буде приводити лише до зміни хвильового вектора електрона k у межах однієї енергетичної зони. Хвильову функцію електрона можна подати у вигляді пакету блохівських хвильових функцій:

, (18.1)

де має гострий максимум при деякому k= k₀. Швидкість руху електрона визначається груповою швидкістю цього пакету

. (18.2)

Зміна енергії електрона за одиницю часу дорівнює роботі зовнішньої сили за одиницю часу.

. (18.3)

Підставляючи (18.2) у (18.3), маємо:

. (18.4)

Диференціюючи за часом функцію , отримаємо

. (18.5)

Порівнюючи (18.4) і (18.5), матимемо

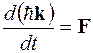. (18.6)

Ми отримали для електрона квазікласичне рівняння руху, в якому роль імпульсу відіграє величина . Величина

(18.7)

називається квазіімпульсом електрона, оскільки його властивості відрізняються від імпульсу вільної частинки. Для того, щоб це показати, отримаємо рівняння руху електрона, в якому фігурує його швидкість. Диференціюючи (18.2) за часом, маємо

. (18.8)

Підставляючи у (18.8) рівняння руху (18.6) і означення тензора оберненої ефективної маси (16.3), маємо

. (18.9)

Рівняння (18.9) є рівнянням руху електрона, в якому фігурує його швидкість і тензор оберненої ефективної маси. Це рівняння відрізняється від класичного рівняння руху вільного електрона, яке виражається через швидкість і масу електрона. Для того, щоб показати цю різницю запишемо рівняння (18.9) в головних вісях тензора . Згідно (16.6) маємо

. (18.10)

Для кристалів кубічної симетрії , а рівняння руху електрона має вигляд

. (18.11)

Таким чином, рівняння руху електрона (18.10) під дією зовнішньої сили схоже із звичайним класичним рівнянням, однак масу електрона в ньому потрібно замінити на ефективну масу, яка може залежати від напрямку руху електрона. Проекції квазіімпульсу електрона в кристалі в загальному випадку дорівнюють . Така відмінність у рівняннях руху вільного електрона та електрона в кристалі зумовлена впливом на електрон періодичного поля кристалу.

Дата добавления: 2017-02-01