Локалізовані стани електрона в кристалі

Часто виникає ситуація, коли на валентний електрон крім періодичного потенціалу ідеального кристалу діє деяке додаткове поле, яке може приводити до локалізованих (зв’язаних) станів електрона в решітці. Це має місце, наприклад, у випадку коли кристал містить домішки атомів іншого сорту, які порушують умову періодичності кристалічного потенціалу. Наявність вільної поверхні кристалу також приводить до появи деякого додаткового поля поблизу поверхні. Таким додатковим полем може бути неоднорідне зовнішнє поле.

Нехай поряд з періодичним потенціалом на валентний електрон діє поле . У цьому випадку гамільтоніан (6.2) електрона у кристалі можна записати у вигляді

= + , (15.1)

де гамільтоніан нульового наближення

= . (15.2)

Нехай нам відомі розв’язки рівняння Шредінгера для ідеального кристалу (див.(7.2))

(15.3)

де - власні функції і власні значення гамільтоніана електрона в ідеальному кристалі. Хвильові функції є функціями Блоха.

Розкладаючи хвильову функцію у рівнянні (6.1) в ряд (див. (10.3))

= (15.4)

і враховуючи (15.1), (15.3) зведемо рівняння (6.1) до системи рівнянь (див. (10.43))

, (15.5)

де

. (15.6)

Виразимо функції Блоха через функції Ван’є . Згідно (12.1)

. (15.7)

Слід зауважити, що рівняння (15.5) є точним.

Розглянемо випадок, коли відрізняється від нуля тільки в межах однієї, наприклад нульової, примітивної комірки кристалу. В цьому випадку у двократній сумі (15.7) достатньо врахувати лише член з . Таким чином, зведемо (15.7) до вигляду

, (15.8)

де - середнє значення потенціалу в межах примітивної комірки, що виноситься за знак інтегралу у виразі (15.7). При розрахунку інтегралу в (15.7) ми скористались умовою ортонормованості функції Ван’є(12.8). Підставляючи (15.8) у (15.5), одержимо

. (15.9)

Вводячи позначення

(15.10)

з рівняння (15.9) одержимо

(15.11)

Підставляючи (15.11) у (15.10) і скорочуючи обидві частини рівності на невідому константу , в результаті маємо

(15.12)

рівняння для енергії 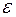електрона в кристалі при заданих значеннях енергії електрона в ідеальному кристалі і збуренні .

Функція

(15.13)

зображена на рис.15.1 суцільними лініями. Корені рівняння (15.12) визначаються точками перетину цих кривих з горизонтальною лінією (позначено штрихами).

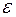Якщо збурення відсутнє, тобто =0, то і значення енергії електрона співпадають із значеннями енергії електрона в ідеальному кристалі. При виникає відщеплення рівня енергії від дна зони. При рівень відщеплюється від верхнього краю зони. Підставляючи (15.11) у (15.4) і враховуючи (14.18), можна показати, що електронні стани, які відповідають відщепленим рівням енергії, є локалізованими. Це порівняно просто можна зробити у випадку одновимірних кристалів, для яких енергії електрона (14.18) має простий вигляд

= , (15.14)

де - дно енергетичної зони, w – напівширина зони.

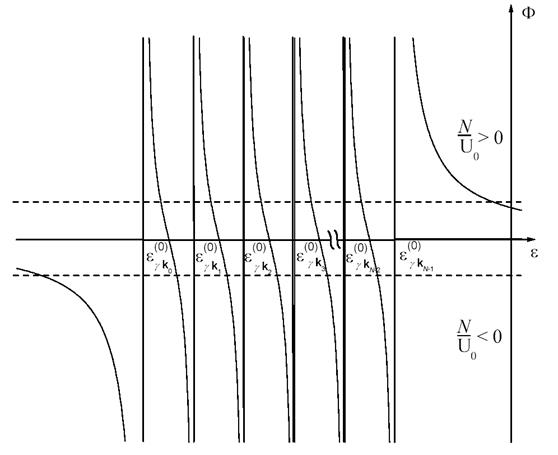
Рис. 15.1. Графічний розв’язок рівняння (15.12).

Хвильовий вектор описується значенням проекції

. (15.15)

Функція (15.13) у цьому випадку набуває вигляду

= , (15.16)

де

. (15.17)

Суму по 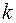для достатньо великого кристалу можна замінити інтегралом згідно формули

. (15.18)

Вираз (15.18) легко одержати, використовуючи (15.15). Підставляючи (15.18) у (15.16) і виконуючи заміну , одержимо

= , (15.19)

якщо . Підставляючи (15.13) у рівняння (15.12) і використовуючи (15.19), в результаті одержимо

. (15.20)

Таким чином, при відщеплюється нижній рівень і тим сильніше, чим більша напівширина зони і відношення ; при відщеплюється верхній рівень.

Перейдемо тепер до розрахунку хвильової функції електрона для стану з енергією . Будемо вважати, що енергетичні зони не перекриваються і скористаємось однозонним наближенням, у якому у виразі для хвильової функції (15.4) електрона в кристалі враховуються внески тільки однієї зони.

Підставляючи (15.11) у (15.4) і враховуючи (7.3), маємо

(15.20)

.

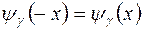При одержанні виразу (15.21) використано наближення ефективної маси, в якому, як буде показано далі, періодичний множник функції Блоха (7.3) дорівнює . Замінюючи у виразі (15.21) суму по 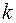інтегралом згідно (15.18), для значення одержуємо

= ,

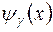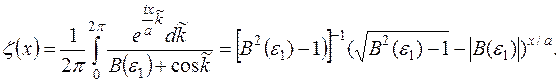(15.22)

Оскільки, згідно (15.17), (15.20) , то функція 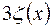має вигляд, показаний на рис.15.2. Тут покладається .

Таким чином, у стані з енергією електрон локалізований в області порушення періодичності кристалічної решітки.

Коли енергетичні зони не перекриваються, часто достатньо скористатись, як зазначалось, однозонним наближенням. У цьому наближенні вираз для хвильової функції електрона (15.4) набуває вигляду

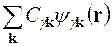= . (15.23)

Підставляючи (15.23) у (6.1) і враховуючи (15.1), (15.3), одержимо

Рис.15.2. Графік функції .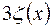

. (15.24)

Скориставшись теоремою Ван’є (11.7) запишемо рівняння (15.24) у вигляді

. (15.25)

Підставивши (15.23) у (15.25), результаті маємо

. (15.26)

Таким чином, в однозначному наближенні рівняння Шредінгера (6.1) замінюється рівнянням (15.26), в якому вже не фігурує періодичний потенціал . Для того, щоб записати оператор у рівнянні (15.26) в явному вигляді, треба знати розв’язок рівняння (15.3) для і замінити хвильовий вектор на оператор (див.(11.2)). Оскільки вигляд оператора є складним, то розв’язок рівняння (15.26) у загальному випадку є неможливим. Розв’язок рівняння (15.26) спрощується, якщо скористатись наближеним виразом для .

Дата добавления: 2017-02-01