Основи теорії зображень

Ряди Фур’є

Розглянемо функцію f (r) радіус-вектора r (5.1) точки кристалу. Нехай f (r) задовольняє циклічним граничним умовам (8.1). Покажемо, що таку функцію можна зобразити у вигляді ряду Фур’є:

, (9.1)

коефіцієнти якого даються виразом

, (9.2)

де d ³ r – елемент об’єму кристалу.

Покажемо, що ряд (9.1) існує, якщо виконується умова ортонормованості

. (9.3)

Для нескінченого кристалу умова (9.3) випливає з властивостей власних функцій самоспряженого оператора імпульсу.

Для обмеженого кристалу виконання умови (9.3) показується безпосереднім розрахунком. Будемо вважати, що умова (9.3) виконується. Доведемо, що ряд (9.1) існує. Для цього домножимо ліву і праву частини рівності (9.1) на функцію

і проінтегруємо по об’єму кристалу. В результаті маємо

. (9.4)

Підставляючи у (9.4) умову ортонормованості (9.3), прийдемо до рівності

. (9.5)

Опускаючи у виразі (9.5) штрих біля вектора k´, приходимо до виразу (9.2), що і треба було довести.

Покажемо тепер виконання умови (9.3) безпосереднім розрахунком.

. (9.6)

При одержанні (9.6) ми використали (5.1), (5.2), (5.4) і вираз для елемента об’єму

,

де Ω₀ дається формулою (5.7). Область інтегрування у правій частині рівності (9.6) зображена на рис.4.

Потрійний інтеграл у правій частині рівності (9.6) зводиться до добутку трьох однократних інтегралів типу

(9.7)

Інтеграл (9.7) розраховано для двох можливих випадків k ₁ = k ´₁ і k ₁ ≠ k ´₁. При розрахунку інтеграла для другого випадку використано (8.6).

Підставляючи (9.7) у (9.6), одержимо

,

тобто прийдемо до виразу (9.3).

Для періодичної функції виконується умова

, (9.8)

де l – вектор вузла прямої решітки (4.1).

Підставляючи (9.1) у (9.8), одержимо

. (9.9)

Прирівнюючи почленно суми у (9.9), бачимо, що рівність (9.9) виконується за умови

,

тобто якщо вектори k пробігають значення векторів вузлів оберненої решітки g (див. (7.7)). Покладаючи у (9.1) k = g, одержимо

, (9.10)

де

. (9.11)

Таким чином, функцію f (r), періодичну з періодом прямої решітки, можна розкласти в ряд Фур’є за векторами оберненої решітки [5].

Розглянемо функцію f _l вектора вузла прямої решітки l (4.1). Нехай f _l задовольняє циклічним граничним умовам (8.1). Покажемо, що таку функцію можна розкласти в ряд Фур’є:

, (9.12)

коефіцієнти якого даються виразом

, (k ÎЗБ), (9.13)

де підсумовування проводиться за всіма вузлами l прямої решітки кристалу.

Підсумовування у виразі (9.12) проводиться за хвильовими векторами k, що належать до зони Бріллюена.

Якби ряд (9.12) був нескінченний, то члени ряду, що відповідають хвильовим векторам k + g, які відрізняються на вектори оберненої решітки g від вектора k ÎЗБ, мали б вигляд

і їх можна було б об’єднати з членом ряду для вектора k ÎЗБ. В результаті ряд набув би вигляду (9.12).

Існування ряду (9.12) пов’язано з виконанням умови ортонормованості

, (k, k ´ÎЗБ). (9.14)

Будемо вважати, що умова (9.14) виконується. Доведемо, що ряд (9.12) існує. Для цього домножимо ліву і праву частини рівності (9.12) на

і підсумуємо по l. В результаті одержимо

. (9.15)

Підставляючи у (9.15) умову ортонормованості (9.14), прийдемо до рівності

, (k ´ÎЗБ). (9.16)

Опускаючи у (9.16) штрих біля вектора k ´, приходимо до виразу (9.13), що і треба було довести.

Покажемо тепер виконання умови (9.14) безпосереднім розрахунком.

. (9.17)

Межі підсумовування у правій частині рівності (9.17) показано на рис.8.1. Потрійна сума у правій частині (9.17) зводиться до добутку трьох однократних сум типу

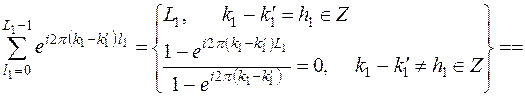
, (9.18)

де h ₁Î Z – ціле число. Суму (9.18) розраховано для двох можливих випадків k ₁– k ₁´ = h ₁Î Z і k ₁– k ₁´≠ h ₁Î Z. У другому випадку суму (9.18) зводимо до суми геометричної прогресії і використовуємо (8.6). Підставляючи (9.18) у (9.17), в результаті одержимо

, (9.19)

де h ₁, h ₂, h ₃ Î Z – цілі числа.

Рівність (9.19) можна записати у вигляді

, (9.20)

де g – вектор вузла оберненої решітки. Якщо у виразі (9.20) вектори k, k ´ належать до зони Бріллюена (k, k ´ÎЗБ), то g = 0 і ми приходимо до виразу (9.14).

Розширимо область означення функції f _k (9.13) і запишемо

,

тобто

. (9.21)

Таким чином, функцію (9.21), періодичну в просторі оберненої решітки, можна розкласти в ряд Фур’є (9.13) за векторами l вузлів прямої решітки.

Для опису стану системи ми використовуємо хвильову функцію , яка є функцією сукупності просторових і спінової координат ξ = x, y, z, σ і часу t. Індекс а біля хвильової функції позначає набір квантових чисел, які визначають стан. У зв’язку з цим індекс а називають індексом стану.

Опис стану за допомогою хвильової функції, що залежить від координат, називається координатним зображенням. Квадрат модуля нормованої хвильової функції координатного зображення визначає густину ймовірності знаходження в даному стані певних значень координат . Літера , що позначає сукупність змінних, від яких залежить хвильова функція, називається індексом зображення. У координатному зображенні оператори виражаються функціями від координат і похідних по координатах. Діючи на функції координатного зображення, оператори перетворюють їх в інші функції того ж зображення.

Розглянемо рівняння на власні функції і власні значення деякого лінійного самоспряженого оператора:

(10.1)

Власні значення такого оператора є дійсними, а власні функції ортогональними. Нормуючи останні, можна записати:

(10.2)

Під інтегруванням по в (10.2) мається на увазі інтегрування по просторових координатах x, y, z і підсумовування по спінових координатах .

Покажемо, що будь–яку функцію 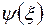можна розкласти по повному набору ортогональних функцій в ряд

(10.3)

коефіцієнти якого даються виразом

. (10.3)

Доведемо, що ряд (10.3) існує. Для цього домножимо ліву і праву частини рівності (10.3) на і про інтегруємо по В результаті одержимо

. (10.5)

Підставляючи в (10.5) умову ортонормованості (10.2), маємо

. (10.6)

Замінюючи у (10.6) індекс n на m, прийдемо до виразу (10.4), що і потрібно було довести.

Ряд (10.3) є узагальненням ряду Фур’є (9.1).

Враховуючи (10.3) і умову ортогональності (10.2), можна записати:

(10.7)

Інтеграл у (10.7) має властивості узагальненого скалярного добутку узагальнених векторів стану , в якому

(10.8)

є проекцією вектора на узагальнений вектор , що відповідає сукупності координат . Для позначення узагальненого скалярного добутку користуються введеними Діраком дужками . Вектор називається вектором «кет», а вектор - вектором «бра». Назви векторів «кет» і «бра» відповідають двом частинам англійського слова «bracket» - дужка.

Із означення (10.7) випливає

(10.9)

Величини у виразах (10.3), (10.4) є проекціями вектора на ортогональні вектори . При цьому вираз (10.4) для проекцій згідно (10.8) можна подати у вигляді

. (10.10)

Враховуючи (10.8), умову ортогональності (10.2) можна записати у формі

. (10.11)

Беручи до уваги ортонормованість векторів і , запишемо

, (10.12)

або, у звичайних позначеннях,

(10.13)

де - дельта-функція Дірака.

Ми одержали нетривіальний результат (10.13), що випливає з умови ортогональності функцій .

Підставляючи (10.8), (10.10) у (10.3), одержимо

(10.14)

Оператор

(10.15)

у виразі (10.14) називається проекційним оператором. Умова

, (10.16)

де I - одиничний оператор, є умовою повноти ортогонального базису

Дія оператора на хвильову функцію координатного зображення визначається виразом

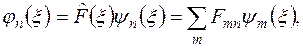(10.17)

де - елемент матриці оператора , що дорівнює

= (10.18)

Запишемо (10.17) у векторному вигляді

(10.19)

де

= . (10.20)

Використовуючи (10.15), (10.16), (10.8), перепишемо (10.20) у вигляді

(10.21)

Порівнюючи (10.18), (10.21), бачимо, що

(10.22)

Отже, матриця оператора у координатному зображенні є діагональною. Діагональні матричні елементи оператора у координатному зображенні дорівнюють оператору (10.17) у зображенні Шредінгера.

Дію оператора на вектори «бра» можна записати у вигляді

(10.23)

де 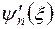дається виразом (10.17).

Підставляючи (10.17) у (10.23), одержимо

(10.24)

Таким чином, при перенесенні дії оператора з вектора «бра» на вектор «кет» він замінюється на ермітово спряжений оператор .

Рівність (10.20) визначає матричні елементи оператора у зображенні, що задається базисними векторами Здійснимо перехід до іншого базису

(10.25)

Можна записати

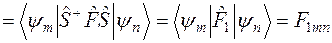, (10.26)

де

(10.27)

Таким чином, матричні елементи оператора у новому зображенні дорівнюють матричним елементам оператора (10.27) у старому зображенні.

При переході від одного ортогонального базису до іншого (10.25)

. (10.28)

Із (10.28) випливає

(10.29)

Оператор, що задовольняє умову (10.29), називається унітарним оператором.

Підставляючи (10.29) у (10.27), для унітарного перетворення базису (10.25), одержимо закон перетворення операторів

(10.30)

Перетворення (10.25) діагоналізує матрицю

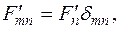(10.31)

якщо матричні елементи оператора перетворень задовольняють систему рівнянь

(10.32)

Величини є власними значеннями оператора .

(10.33)

Рівняння (10.32) можна одержати, підставляючи (10.25) у (10.33) і домножуючи на . Вираз (10.25) відповідає (10.14), якщо у першому опустити індекс n і штрих, і замінити S на C. У результаті рівняння (10.33) на власні функції і власні значення оператора набуває вигляду

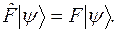(10.24)

Рівняння (10.34) у векторній формі можна записати у матричному вигляді (див. (10.32))

, (10.35)

де - коефіцієнти розкладу вектора стану (10.14) по базисних векторах , що є власними векторами деякого лінійного самоспряженого оператора

(10.36)

Слід зауважити, що перетворення (10.25), (10.32) діагоналізує квадратичну форму

Оператор у (10.34) можна зобразити на базисі векторів у вигляді

(10.37)

У справедливості виразу (10.37) можна переконатись, використовуючи (10.16), (10.15) (10.20). Вводячи позначення , надамо виразу (10.37) більш короткої форми

(10.38)

Розглянемо тепер задачу на власні вектори і власні значення гамільтоніана системи . У цьому випадку у виразі (10.34) покладемо = , . Нехай оператор можна записати у вигляді

(10.39)

де - гамільтоніан нульового наближення, для якого відомі розв’язки рівняння

(10.40)

Покладаючи у виразі (10.36) , систему рівнянь (10.35) запишемо у формі

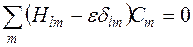(10.41)

Підставляючи = , (10.39), (10.40) у (10.20), маємо

(10.42)

Враховуючи (10.42), приведемо (10.41) до вигляду

(10.43)

Умовою існування розв’язку системи рівнянь (10.41) є

(10.44)

Кожному кореню рівняння (10.44) відповідає свій розв’язок системи рівнянь (10.41) і свій вектор стану (10.14)

(10.45)

Величини , є розв’язком рівняння (10.33) при = , для власних значень гамільтоніана системи.

Матриця системи рівнянь (10.41) має у більшості випадків нескінченний ранг, тому знаходження точного розв’язку системи є часто неможливим. У цих випадках перевагу надають системі рівнянь у вигляді (10.43), наближений розв’язок якої знаходять методом теорії збурень.

Дата добавления: 2017-02-01