Обернена решітка кристалу

Скалярний добуток двох векторів, що задані на ортогональному базисі, виражається, як відомо, через суму добутків їх проекцій. Оскільки в теорії твердого тіла зручно користуватись не ортогональним базисом a _і, то для надання скалярному добутку двох векторів, який часто застосовується в теорії, того ж вигляду, що і для ортогонального базису, вводять допоміжний базис b _і.

При цьому покладають, що у скалярному добутку векторів 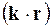вектор, який стоїть справа, зображають на базисі кристалічної решітки a _і:

, (5.1)

а вектор, який стоїть зліва – на допоміжному базисі b _і:

. (5.2)

Якщо означити базисні вектори b _і умовою

, (5.3)

де – символи Кронекера, то скалярний добуток векторів 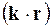набуває вигляду

, (5.4)

тобто такого ж вигляду, як і для ортогонального базису. Множник 2 π у правій частині рівності (5.3) ставиться для зручності.

Вектори

(5.5)

з цілими координатами g_i називають векторами вузлів оберненої решітки, а вектори b _і – основними векторами оберненої решітки.

Для тривимірної решітки система рівнянь (5.3) має розв’язок:

, , , (5.6)

де

(5.7)

– об’єм примітивної комірки прямої решітки.

Паралелепіпед, що побудований на трьох основних векторах оберненої решітки b _і, називається основною коміркою оберненої решітки. Його об’єм

. (5.8)

Властивості оберненої решітки.

1. Вектор оберненої решітки g (5.5) перпендикулярний до сімейств площин прямої решітки з індексами Міллера
(h ₁, h ₂, h ₃), якщо координати вектора задовольняють умові:

, , , (5.9)

m – деякий спільний множник, що є цілим числом.

Для доведення розглянемо одну площину із сімейства
(h ₁, h ₂, h ₃). На рис. 5.1 показано точки перетину цієї площини з координатними вісями. Згідно означення індексів Міллера, координати цих точок дорівнюють (p / h ₁, 0,0), (0, p / h ₂, 0),
(0, 0, p / h ₃), де множник p вибирається таким чином, щоб індекси Міллера (h ₁, h ₂, h ₃) були цілими числами.

Рис.5.1. Площина сімейства площин (h ₁, h ₂, h ₃).

Умовою перпендикулярності вектора g (5.5) до площини (h ₁, h ₂, h ₃) є перпендикулярність вектора g до двох непаралельних векторів

, ,

що лежать в цій площині, тобто:

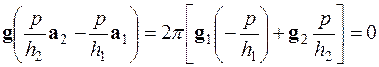, (5.10)

.

Умови (5.10) виконуються, якщо виконується умова (5.9), що і треба було довести.

2. Модуль вектора оберненої решітки g (5.5) з координатами:

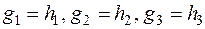(5.11)

дорівнює:

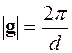, (5.12)

де d – найменша відстань між площинами сімейства
(h ₁, h ₂, h ₃).

Для доведення розглянемо

, (5.13)

де N – ціле число, l_g – проекція вектора прямої решітки l на напрям вектора оберненої решітки g.

Для векторів вузлів прямої решітки , що лежать на сусідній площині, можна записати

. (5.14)

Враховуючи, що найменша відстань між площинами дорівнює

(5.15)

і використовуючи (5.13), (5.14), одержимо (5.12).

Дата добавления: 2017-02-01