Локальне наближення для обмінного потенціала

Запишемо ефективний потенціал обмінної взаємодії у вигляді (див.(2.14))

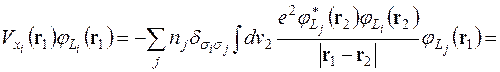
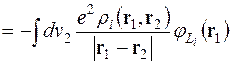, (3.1)

де введена обмінна зарядова густина

. (3.2)

Обмінний потенціал для газу вільних електронів.

Використаємо в якості одноелектронних хвильових функцій функції вільного електрона

, (3.3)

де Ω – об’єм системи. Електронні стани характеризуються квантовими числами (, де – імпульс Фермі). При нульовій температурі Т = 0 К число електронів дорівнює

. (3.4)

Множник 2 у правій частині рівності (3.4) враховує число значень проекції спіна на вісь z. Замінюючи у виразі (3.4) суму по інтегралом згідно формули (буде встановлена в подальшому)

, (3.5)

прийдемо до виразу для електронної густини

. (3.6)

Звідси

, (3.7)

де – густина електронів з однаковими проекціями спіна.

Вирахуємо обмінний потенціал (3.1), вважаючи, що електрон знаходиться в початку координат 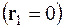. Підставляючи (3.3) в (3.1) і інтегруючи, одержимо

. (3.8)

Використовуючи (3.5), надамо виразу (3.8) вигляд

, (3.9)

де

, (3.10)

Ефективний обмінний потенціал, усереднений за всіма станами, дорівнює

, (3.11)

Підставляючи (3.7) в (3.11), в результаті одержимо

. (3.12)

Обмінний потенціал Слетера.

Слетер запропонував використовувати потенціал (3.12) для опису обмінної взаємодії не тільки вільних електронів, але і для електронів в системах з неоднорідним розподілом електронної густини:

. (3.13)

Якщо розрахунки проводяться без врахування спінової поляризації електронних станів за умови , то обмінний потенціал Слетера записується у вигляді

. (3.14)

де

(3.15)

є повна електронна густина.

Обмінний потенціал Гаспара – Кона – Шема.

Локальний обмінний потенціал вираховувався і методом, що ґрунтується на методі функціонала електронної густини, суть якого полягає в наступному. Повна енергія Е електронної системи є деяким потенціалом електронної густини (3.15). Виділяючи у повній енергії системи Е вклади кінетичного, кулонівського і обмінного членів, одержимо (див.(2.8))

, (3.16)

Враховуючи (2.9), (2.8), (2.2), замінимо варіаційну похідну функціонала кінетичної енергії (3.16) оператором кінетичної енергії:

.

З принципу мінімума повної енергії системи як функціонала електронної густини одержимо варіаційне рівняння для одноелектронної хвильової функції

. (3.17)

в якому

. (3.18)

Для газу електронів, густина якого змінюється повільно, можна застосувати наближення

, (3.19)

де – обмінна енергія, що припадає на один електрон в однорідному електронному газі. Підставляючи (3.19) в (3.18), одержимо

. (3.20)

Гаспар, Кон і Шем замінили у (3.19) його статистичним наближенням (3.14) і в результаті одержали

. (3.21)

Врахування електронних кореляцій.

У методі Хартрі – Фока враховуються кореляції у русі електронів з однаковими проекціями спінів, що зумовлює появу обмінного члена. Однак між електронами існує кулонівська взаємодія (відштовхування одноіменних зарядів), внаслідок якої положення одного електрона залежить від положення інших. У наближенні Хартрі – Фока кожний електрон рухається незалежно від інших в деякому ефективному полі, дія якого на електрон еквівалентна усередненій дії на нього всіх інших електронів. Це випливає з того, що хвильова функція системи електронів записується у вигляді хвильової функції (2.3) системи невзаємодіючих частинок. У дійсності хвильова функція повинна відображати зменшення ймовірності знаходження електронів у тісному сусідстві, що веде до утворення так званої кореляційної дірки. Зокрема, завдяки нехтуванню електронними кореляціями в обмінному потенціалі (3.9) для газу вільних електронів виникає логарифмічна особливість на рівні Фермі. Оскільки при переході до статистичного наближення (3.12) ця особливість зникає, то кажуть, що воно “частково враховує кореляцію”. У зв’язку з цим одержане локальне наближення для обмінного потенціалу вірніше називати обмінно-кореляційним потенціалом. Однак коректно врахувати кореляційні ефекти можна лише у рамках багато електронної теорії (див. розділ 4). Врахування кореляційних ефектів приводить до появи у правих частинах виразів (3.19), (3.21) поправок, що залежать від електронної густини.

Гелл-Ман і Бракнер запропонували метод розрахунку поправки до енергії системи, що зумовлена електрон-електронною взаємодією, шляхом підсумовування членів у всіх порядках теорії збурень, які дають основний внесок у випадку високої густини електронного газу.

Згідно результату Гелл-Мана і Бракнера, вираз для обмінно-кореляційної енергії має вигляд [4,5]:

(3.22)

де

, (3.23)

r – електронна густина, a ₀ – радіус Бора, r_s – радіус сфери, рівновеликої за об’ємом об’єму, який приходиться на один електрон.

Вігнер, здійснивши інтерполяцію між граничними випадками високої і малої густини, одержав:

(3.24)

Перший доданок в квадратних дужках в (3.22) і (3.24) приводить до обмінного потенціалу Гаспара – Кона – Шема, решта описує поправки на електронні кореляції. У відповідності з цим обмінно-кореляційний потенціал представимо у вигляді суми потенціалів Гаспара – Кона – Шема і деякої добавки, що залежить від r_S:

. (3.25)

Використовуючи (3.18), в результаті із (3.22) одержимо:

. (3.26)

Аналогічно з (3.18), (3.24), одержимо:

. (3.27)

Внесок електрон-електронної взаємодії в енергію системи можна визначити, зводячи його до екранування зовнішнього потенціалу електронним газом і розраховуючи діелектричну проникність кристалу. В наближенні самоузгодженого поля, відомому ще як наближення випадкових фаз, Хедін і Лундквіст отримали обмінно-кореляційний потенціал у вигляді (3.25), де

. (3.28)

Параметри c^P і r^P, що входять в цю формулу, мають значення c^P =0,0504, r^P =30.

Обмінно-кореляційний потенціал (3.25) можна представити у вигляді потенціалу Слетера з залежним від r_S множником :

(3.29)

При цьому

, (3.30)

В наближенні хаотичних фаз з врахуванням спінової поляризації локальний обмінно-кореляційний потенціал можна подати у вигляді [4]

. (3.31)

Перший доданок – обмінно-кореляційний потенціал Гаспара – Кона – Шема, записаний в спін-поляризованому вигляді

, (3.32)

виражається формулою (3.28), а

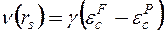, (3.33)

де , , , , c^F =0,0254, r^F =75, c^P =0,0504, r^P =30.

Вирази для обмінно-кореляційного потенціалу, що наведені вище, одержано в локальному наближенні, яке є справедливим, як вже зазначалось, для випадку однорідного розподілу електронної густини. Зазначене наближення відоме ще як наближення локальної густини.

Вихід за рамки наближення локальної густини.

Для того, щоб врахувати неоднорідність в розподілі електронної густини в методі функціонала електронної густини, потрібно виконати градієнтний розклад r (r), тобто розкласти r (r) в ряд за степенями при деякому середньому значенні електронної густини r. Обмежуючись членами другого порядку, для обмінно-кореляційного потенціалу матимемо [4]:

. (3.34)

– наближення для обмінного потенціалу.

Вибір обмінного потенціала суттєво впливає на результати розрахунку електронної структури конкретних систем. Як свідчать результати числових розрахунків, для одних елементів і сполук слід застосовувати потенціал (3.13), а для інших – потенціал (3.21). У цій ситуації має сенс ввести в локальний обмінний потенціал параметр a, який для різних атомів приймає різні значення.

Потенціал

. (3.35)

називають обмінним потенціалом у – наближенні. При a = 1 він переходить у потенціал (3.13), а при a = 2/3 – у потенціал (3.21). Значення параметра a підбирають шляхом мінімізації повної енергії Е (a) (2.8) як функції параметра a, від якого у (2.8) залежать одноелектронні хвильові функції , що знаходяться з рівняння Хартрі – Фока (2.13) з обмінним потенціалом 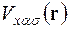(3.35).

У розрахунках часто наближено покладають, що залежність параметра a (z) від порядкового номера елемента z періодичної системи є гладкою і користуються значеннями a, що розраховані для легких, середніх та тяжких атомів. Так для атомів з порядковим номером z, що відповідає середині періодичної системи, a @ 0,75.

Враховуючи (2.13), (2.14), (3.1), (3.35), (3.15), запишемо рівняння Хартрі – Фока у вигляді

, (3.36)

де

(3.37)

– потенціальна енергія електрона в полі нерухомих ядер,

(3.38)

– кулонівський потенціал електронного заряду,

. (3.39)

– обмінний потенціал,

, (3.40)

– густина електронів з проекцією спіна σ,

, (3.41)

– повна електронна густина.

Дата добавления: 2017-02-01