Адіабатичне наближення

При квантовомеханічному описі твердих тіл доводиться розглядати системи, що складаються з великого числа електронів і атомних ядер. Оскільки маси ядер в декілька тисяч разів більші маси електрона, то в середньому вони рухаються значно повільніше, ніж електрони. У зв’язку з цим існує можливість наближеного опису твердих тіл, де в нульовому наближенні ядра вважаються нерухомими, а в наступних наближеннях рух ядер враховується методами теорії збурень. Такий наближений опис називається адіабатичним наближенням.

Якщо не враховувати релятивістські ефекти та процеси в твердому тілі, що пов’язані з ядерними перетвореннями, то оператор Гамільтона системи можна записати у вигляді [1-3]

, (1.1)

де

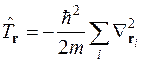(1.2)

– оператор кінетичної енергії електронів, – радіус-вектор і -го електрона, m – маса електрона, 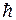– постійна Планка;

(1.3)

– оператор кінетичної енергії ядер з координатами і масами ;

(1.4)

– оператор потенціальної енергії взаємодії електронів і ядер,

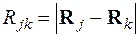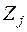, , , – порядковий номер j -го ядра, , – сукупність координат електронів і ядер відповідно, е – заряд електрона.

В адіабатичному наближенні оператор кінетичної енергії важких частинок 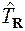(1.3) розглядається як збурення.

Таким чином, запишемо оператор (1.1) у вигляді

, (1.5)

де

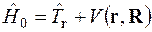. (1.6)

У нульовому наближенні рівняння Шредінгера має вигляд

. (1.7)

Тут – не змінні диференціального рівняння, а параметри, що визначають потенціальне поле ядер. У зв’язку з цим власні функції і власні значення рівняння (1.7) залежать від як від параметрів. Таким чином, функції описують стани руху електронів при фіксованому значенні координат ядер.

Стаціонарні стани системи описуються рівнянням

(1.8)

в якому – оператор Гамільтона (1.1). Розв’язок рівняння (1.8) можна шукати у вигляді

(1.9)

Підставляючи (1.9) в (1.8), використовуючи рівняння нульового наближення (1.7), помножуючи на та інтегруючи по координатах електронів, приходимо до системи рівнянь

, (1.10)

де оператор

, (1.11)

, , .

Система рівнянь (1.10) є точною. Оскільки оператор (1.11) містить малі параметри 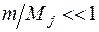, то систему рівнянь (1.10) можна розв’язувати за методом послідовних наближень. У нульовому (адіабатичному) наближенні права частина рівняння (1.10) покладається рівною нулеві. Таким чином, в адіабатичному наближенні система рівнянь (1.10) розпадається на систему незалежних рівнянь

(1.12)

для кожного стану руху електронів, що визначається квантовими числами m.

З (1.12) випливає, що рух ядер описується потенціальною енергією , яка дорівнює енергії електронів рівняння (1.7) при фіксованих положеннях ядер.

В адіабатичному наближенні хвильова функція системи (1.9) зводиться до добутку

. (1.13)

Таким чином, кожному стану електронів, що визначається квантовими числами m, відповідають стани ядер, які відрізняються квантовими числами .

Користуючись теорією збурень, можна показати, що адіабатичне наближення можна застосувати за умови

, m ≠ n. (1.14)

Дослідження розв’язків рівняння (1.12) показує, що достатньою умовою для застосовності адіабатичного наближення є малість частот коливань ядер 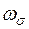у порівнянні з частотами, що відповідають електронним станам, тобто

. (1.15)

Дата добавления: 2017-02-01