Густина електронних станів

Рівняння Шредінгера для електрона в кристалі, який у довільному випадку містить домішки, можна подати у вигляді (див. (10.40)):

(19.1)

Для ідеального кристалу індекс стану a згідно (7.2) дорівнює .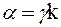

Повна електронна енергія кристалу без урахування електрон-електронної взаємодії дорівнює

, (19.2)

де – число заповнення стану, яке приймає значення 1 чи 0. Середнє значення повної електронної енергії кристалу дорівнює

. (19.3)

Тут – функція розподілу Фермі:

, (19.4)

де – рівень Фермі, k_Б – постійна Больцмана, Т – температура.

Для розрахунку середнього значення повної електронної енергії кристалу (19.3) необхідно розрахувати суму по індексах стану a від функції . Легко показати, що ця сума дорівнює

. (19.5)

Тут – густина електронних станів (число електронних станів на одиничний інтервал енергії), що описується виразом:

, (19.6)

де – d -функція Дірака. Крім того, згідно (19.5), густину станів можна подати у вигляді:

, (19.7)

де – число електронних станів на інтервал енергії , яке дається виразом:

. (19.8)

Одержимо вираз для густини електронних станів ідеального кристалу. Згідно (19.8) маємо:

. (19.9)

Таким чином, для розрахунку отримаємо формулу для підсумовування по k деякої функції f (k). Використовуючи (8.5), (8.6), одержимо:

.(19.10)

Оберемо елемент об’єму d ³ k в k -просторі у формі елементарної комірки оберненої решітки. Тоді маємо b

. (19.11)

При одержанні останньої рівності у формулі (19.11) використано (5.8).

Підставляючи (19.11) в (19.10) маємо:

, (19.12)

де – об’єм кристалу.

Формула (19.12) встановлює правило заміни суми по k інтегралом по об’єму в оберненому просторі.

Підставляючи (19.12) у (19.9), одержимо

. (19.13)

Інтегрування у виразі (19.13) проводиться по об’єму оболонки в оберненому просторі, яка обмежена двома поверхнями постійної енергії:

, . (19.14)

Враховуючи зазначене, інтеграл у виразі (19.13) зводимо до інтегралу з елементом об’єму у формі паралепіпеда, висота якого дорівнює товщині оболонки dk_n, а площа основи – .

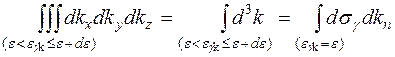. (19.15)

У виразі (19.15) k_n – проекція хвильового вектора на напрямок зовнішньої нормалі до поверхні постійної енергії. Диференціюючи перше рівняння (19.14), маємо

(19.16)

Тут враховано, що вектор градієнта паралельний зовнішній нормалі до поверхні постійної енергії. Підставляючи (19.16) в (19.15), одержимо:

. (19.17)

Використовуючи (19.17), перепишемо вираз (19.13) у вигляді:

. (19.18)

Підставляючи (19.18) у (19.7), в результаті одержимо вираз для густини електронних станів ідеального кристалу:

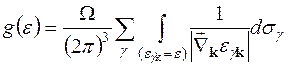. (19.19)

Для прикладу розрахуємо густину електронних станів кристалу в наближенні ефективної маси.

Рівняння поверхні постійної енергії електрона в кристалі (19.14) у цьому випадку, згідно виразу (16.9), має форму сфери, а вектор градієнта – паралельний вектору k, тому

. (19.20)

Індекс стану у виразі (19.19) включає індекс проекції спіну електрона на вісь z. Оскільки рівняння поверхні постійної енергії (19.14) у цьому випадку, згідно виразу (16.9), від індексу проекції спіну не залежить, то підсумовування по у виразі (19.19) зводиться до множення на число 2. Підставляючи (19.20) в (19.19), з врахуванням зазначеного одержимо:

. (19.21)

Враховуючи, що інтеграл по поверхні сфери у виразі (19.21) дорівнює , а, згідно (16.9),

, (19.22)

в результаті одержуємо:

. (19.23)

Таким чином, в наближенні ефективної маси, а також майже вільних електронів густина одноелектронних станів кристалу зростає зі збільшенням енергії за законом .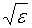

Дата добавления: 2017-02-01