Коливання атомів одновимірної решітки

У випадку одновимірної кристалічної решітки розв’язок рівняння руху можна знайти аналітично.

Розглянемо спочатку приклад простої одновимірної кристалічної решітки з одним атомом масою M на примітивну комірку. Нехай відстань між атомами дорівнює a. Для спрощення обмежимось лише взаємодією найближчих сусідів і будемо вважати, що взаємоперпендикулярні зміщення атомів є незалежними. В такому випадку достатньо розглянути зміщення атомів тільки вздовж однієї вісі координат x, що напрямлена вздовж ланцюжка атомів (рис.24.1). Хрестиками на рисунку рис.24.1 позначено вузли кристалічної решітки (рівноважні положення атомів), а кружечками — положення атомів в довільний момент часу.

Рис.24.1 Проста одновимірна решітка

Умова (21.13) для силових сталих кристалу в цьому випадку має вигляд

. (24.1)

У рівнянні (24.1) індекси вісі координат a = x і сорту атома i =0 опущено. Покладаючи

, (24.2)

з (24.1) одержимо

(24.3)

Динамічна матриця (22.3) в цьому випадку дорівнює

(24.4)

Рівняння руху кристалічної решітки (22.2) має вигляд

, (24.5)

а умовою розв’язку (22.6) цього рівняння є

. (24.6)

Підставляючи (24.4) в (24.6), одержимо

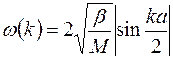. (24.7)

Залежність (24.7) задовольняє умові (23.12). Таким чином, вираз (24.7) описує закон дисперсії для акустичних коливань одновимірної простої кристалічної решітки (рис. 24.2).

Рис.24.2 Закон дисперсії для акустичних коливань одновимірної простої кристалічної решітки

Перейдемо тепер до розгляду коливань одновимірної складної кристалічної решітки з двома атомами масою M ₀, M ₁ на примітивну комірку (рис.24.3). Хрестиками на рисунку рис.24.3 позначено вузли кристалічної решітки, положення яких співпадають з рівноважним положенням атомів сорту i =0 масою M ₀, а вертикальними рисочками — рівноважне положення атомів сорту i =1 масою M ₁. Параметр кристалічної решітки позначимо через a '. Як і для простої одновимірної решітки, врахуємо лише взаємодію найближчих сусідів і будемо вважати, що взаємоперпендикулярні зміщення атомів є незалежними. Як і раніше, в такому випадку достатньо розглянути зміщення атомів тільки вздовж однієї вісі координат x, що напрямлена вздовж ланцюжка атомів (рис.24.3).

Рис.24.3 Складна одновимірна решітка

Умова (21.13) для силових сталих кристалу в цьому випадку має вигляд

, (24.8)

. (24.9)

У рівняннях (24.8), (24.9) індекс вісі координат a = x опущено. Покладаючи

, (24.10)

, (24.11)

з рівнянь (24.8), (24.9) одержимо

. (24.12)

Елементи динамічної матриці (22.3) в цьому випадку даються виразами:

, (24.13)

, (24.14)

, (24.15)

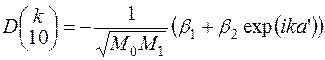. (24.16)

Рівняння руху кристалічної решітки (22.2) має вигляд

, (i =0,1), (24.17)

а умовою розв’язку (22.6) цього рівняння є

. (24.18)

Використовуючи (24.13)–(24.16), знаходимо розв’язки рівняння (24.18):

, (24.19)

, (24.20)

де введено позначення

, (24.21)

. (24.22)

З виразів (24.19), (24.20) випливає, що

, , (24.23)

, . (24.24)

Залежність (24.19), згідно (24.23), задовольняє умові (23.12) і описує закон дисперсії для акустичної гілки коливань (рис.24.24). Залежність (24.20), згідно (24.24), задовольняє умові (23.20) і описує закон дисперсії для оптичної гілки коливань.

Із системи рівнянь руху (24.17) знайдемо

. (24.25)

У граничному випадку k =0 для першого розв’язку (24.19) маємо

. (24.26)

Порівнюючи (24.23), (24.26) з (23.12), (23.14) відповідно, переконуємось, що перший розв’язок (24.19) є законом дисперсії для акустичної гілки коливань.

У граничному випадку k =0 для другого розв’язку (24.20) маємо

, (24.27)

де – зміщення атома сорту i для гілки коливань j =2 при k =0.

Порівнюючи (24.24), (24.27) з (23.20), (23.19) відповідно, бачимо, що другий розв’язок (24.20) є законом дисперсії для оптичної гілки коливань.

Закон дисперсії для акустичної і оптичної гілок коливань одновимірної кристалічної решітки з двома атомами на примітивну комірку показано на рис.24.4а.

Рис.24.4 Закон дисперсії коливань атомів складної одновимірної решітки

Замінимо атоми в такій решітці атомами одного сорту. В цьому випадку

, . (24.28)

З виразів (24.21), (24.22), враховуючи (24.28), маємо:

, . (24.29)

Підставляючи (24.29) у (24.19), (24.20), одержимо:

, (24.30)

. (24.31)

Закон дисперсії для такої решітки зображено на рис.24.4б.

При заміні атомів решітки атомами одного сорту вона стає простою. Закон дисперсії для простої одновимірної решітки дається виразом (24.7). На перший погляд здається, що два підходи до опису коливань однієї і тієї ж решітки дали різні результати. Насправді ж вирази (24.30), (24.31) і (24.7) узгоджуються між собою. Для того, щоб це показати врахуємо, що при описі коливань за допомогою складної решітки параметр кристалічної решітки , де a – відстань між атомами, що фігурує у виразі (24.7). Враховуючи це, перепишемо (24.30), (24.31) у вигляді

, (24.32)

. (24.33)

У виразах (24.32), (24.33) k змінюється у межах , а у виразі (24.7) — у межах . Перша залежність (24.32) співпадає з залежністю (24.7) на інтервалі . Замінюючи у виразі (24.33) проекцію k вектора k на проекцію еквівалентного вектора, матимемо

,

де k ' змінюється у межах . Таким чином, бачимо, що на цьому інтервалі другий вираз (24.33) співпадає з виразом (24.7). Звідси випливає, що вирази закону дисперсії за допомогою формул (24.32), (24.33) і формули (24.7) є еквівалентними.

Дата добавления: 2017-02-01