Примеры решения задач

Пример 1. Определить число узлов, приходящееся на одну элементарную ячейку в базоцентрированной ромбической решетке.

Решение. Выделим элементарную ячейку в кубической решетке (рис. 3.1) и определим, скольким соседним элементарным ячейкам принадлежит той или иной узел выделенной ячейки. Узлы в углах принадлежат одновременно восьми элементарным ячейкам, узлы на гранях принадлежат только двум ячейкам. Поэтому общее число узлов, приходящееся на одну базоцентрированную ячейку,

n =1/8×8+1/2×2=2 узла.

`

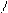
Рис. 3.1. Элементарная ячейка

Пример 2. Определить число элементарных ячеек кристалла меди объемом V =1 см³.

Решение. Число элементарных ячеек кристалла определяется из выражения (3.4)

z = ρkN_aV / nM.

Поскольку ячейка состоит из одинаковых атомов, то k =1. Плотность меди считаем известной (ρ= 8,93×10³ кг/м³). Малярная масса вещества определяется с помощью периодической таблицы Менделеева (М=63,55×10^-3 кг/моль). Медь относится к кристаллам гранецентрированной кубической решетки, следовательно ее ячейка содержит 4 атома (n =4). Подставив данные в расчетную формулу, получим

z =8,93×10³×1×6,02×10²³×1×10^-6/(4×63,55×10^-3)=2,11×10²².

Пример 3. Определить параметры решетки а и расстояние d между ближайшими соседними атомами кристалла кальция.

Решение. Поскольку кальций имеет ГЦК-решетку, то объем элементарной ячейки V = a ³. С другой стороны, объем элементарной ячейки может быть найден из соотношения (3.2)

V = V_M / Z_M.

В результате можно записать с учетом (3.4)

a = .

Подставляя значения величин n, М и N_a в формулу и проводя вычисления, получим

а =556 пм.

Расстояние между ближайшими соседними атомами находится из простых геометрических соображений

d = a / .

d =393 пм

Пример 4. Написать индексы направления прямой, проходящие через узлы [[110]] и [[011]] кубической примитивной решетки.

Решение. Рассмотрим аналитический метод решения. Напишем в общем виде уравнение прямой, проходящей через две точки в пространстве, с индексами узлов [[m₁ n₁ p₁]] и [[m₂ n₂ p₂]

Величины, стоящие в знаменателях, пропорциональны направляющим косинусам прямой. Но так как эти величины целочисленны (по определению), то они и будут являться индексами направления. Подставляя в знаменатели данного выражения значения индексов узлов, получим:

m₂-m₁=0-1=-1

n₂-n₁=1-1=0

p₂-p₁=1-0=1

Таким образом искомые индексы направления [101].

Возможен также графический способ решения.

Пример 5. Найти индексы Миллера для плоскости, содержащей узлы с индексами [[2 0 0]], [[0 1 0]] и [[0 0 2]].

Решение. Анализ условий задачи показывает, что известны отрезки, отсекаемые плоскостью на осях координат. Отрезки выражаются в единицах постоянной решетки соответственно 2,1,2. В соответствии с общим правилом нахождения индексов Миллера запишем обратные значения данных чисел ½; 1/1; ½ и приведем их к наименьшему целому кратному этих чисел (умножив их на 2). Полученная совокупность значений и есть искомые индексы Миллера – (1 2 1).

Можно воспользоваться аналитическим методом, решая задачу об отыскании уравнения плоскости, проходящей через три точки с заданными индексами Миллера. Особенно удобен этот способ в том случае, когда точки не лежат на осях координат.

Дата добавления: 2017-02-01