Примеры решения задач

Пример 1. Электрон, начальной скоростью которого можно пренебречь принял ускоряющую разность потенциалов: 1) 100 В; 2) 500 кВ. Определить длину волны электрона.

Решение: В первую очередь необходимо установить, является ли частица ли частица релятивистской, т.е. Т ≈ Е ₀ или классической Т << Е ₀, где Т – кинетическая энергия частицы, а Е ₀ – энергия покоя.

В первом случае получаем соотношение:

Частица является нерелятивистской и можно воспользоваться выражением (3.8)

.

Во втором случае получим соотношение:

;

то есть частица релятивистская и необходимо воспользоваться выражением (3.9).

Пример 2. Кинетическая энергия электрона в атоме водорода имеет величину порядка T =10 эВ. Используя соотношение неопределенностей оценить минимальные размеры атома.

Решение: Соотношение неопределенностей для координаты и импульса имеет вид, в частности:

Пусть атом имеет линейные размеры l, тогда электрон атома будет находиться где-то в приделах области с неопределенностью . Соотношение неопределенностей в этом случае можно записать в виде:

Физически разумная неопределенность импульса не должна превышать величины самого импульса, т.е. . Импульс связан с кинетической энергией известным соотношением:

Заменим Р значением 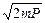(такая замена не увеличит l), и перейдем от неравенства к равенству:

Подставив числовые значения и проведя вычисления, получим:

l _min=124 пм.

Пример 3. Определить фазовую скорость волны де Бройля, свободно движущейся с постоянной скоростью υ электрона в нерелятивистском и релятивистском случаях.

Решение: Известно, что υ_ф = ω / k, ω =2 πν, k =2 π / λ. Можно записать:

1). υ << c – нерелятивистский случай.

2). υ ≈ c – релятивистский случай.

Пример 4. Сравнить минимальные неопределенности координаты электрона и винтовочной пули (9 г), если неопределенность скоростей у них одинакова – 5 м/с.

Решение: В случае минимума неопределенностей в (3.10) переходим к равенству:

.

Подставив численные значения и проведя вычисления, получим:

– для электрона: ,

– для пули:

Пример 5. Электрон находится в бесконечно глубокой потенциальной яме шириной L. Вычислить вероятность того, что электрон, находящийся в возбужденном состоянии (n =2), находится в первой четверти потенциальной ямы.

Решение: Вероятность W обнаружить частицу в интервале определяется равенством (3.19). Нормированная собственная волновая функция, описывающая состояние электрона в потенциальной яме (3.18). В итоге можно записать выражение:

или

Запишем соотношение:

и представим интеграл в виде:

Пример 6. Монохроматический поток электронов (Е = 50 эВ) подает на низкую потенциальную ступень бесконечной ширины. Определить высоту потенциальной ступени U ₀, если известно, что 5% падающих на ступень электронов отражается.

Решение: Коэффициент отражения R от низкой потенциальной ступени выражается формулой (3.22).

В области I кинетическая энергия электрона Е и волновое число связаны соотношением:

В области II волновое число выражается соотношением:

С учетом и можно записать:

Преобразуя последнее выражение, можно записать:

Подставляя в данное выражение значения величин, и произведя вычисления, найдем:

Пример 7. Электрон с энергией E = 6,2 эВ движется в положительном направлении оси Х. Высота потенциального барьера U ₀= 6,5 эВ. При какой толщине барьера вероятность прохождения электрона через нее будет равна 0,1.

Решение: Вероятность W прохождения частицы через потенциальный барьер смыслу совпадает с коэффициентом прозрачности D. C учетом выражения (3.24) можно записать:

.

Логарифмируя это выражение, получим:

или

Подставим необходимые величины (в системе СИ), произведем вычисления и получим:

d ≈ 0,01 нм.

Пример 8. Электрон в атоме водорода перешел со второго энергетического уровня на четвертый. Определить длину волны, энергию рожденного в этом случае фотона.

Решение: Переход связан с убыванием энергии (см. 3.25)

С другой стороны известно соотношение:

Из приведенных выражений можно определить длину волны:

Подставив в расчетную формулу данные и проведя необходимые вычисления, получим:

.

Пример 9. Определить максимальную энергию фотона, который может возникать в кристалле NaCl. Температура Дебая Т_g =320К. Определить длину волны фотона с такой энергией.

Решение: Энергия фотона определяется температурой среды

E_Ф = kТ_g.

Известно (3.27), что энергия фотона составляет

.

Длина волны фотона

Вычисления дают величины:

Е_Ф =28 мэВ, λ =45 мкм.

Дата добавления: 2017-02-01