Основные справочные формулы

· Формула де Бройля, выражает связь длины волны 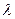с импульсом р движущейся частицы, для двух случаев:

а). в нерелятивистском случае (p = m ₀ V), если V << c

; (3.6)

б). в релятивистском случае (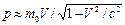), если V → c,

, (3.7)

где: h – постоянная Планка;

m ₀ – масса покоя частицы;

V – скорость частицы;

с – скорость света в вакууме.

· Связь длины волны де Бройля с кинетической энергией Т частицы

а) для нерелятивистского случая

; (3.8)

б) для релятивистского случая

, (3.9)

где Е ₀= m ₀ с – энергия покоя.

· Соотношения неопределенностей Гейзенберга имеют вид

(3.10)

(3.11)

где D P_x – неопределенность проекций импульса на ось х;

Δ E – неопределенность энергии частицы;

Δ t – неопределенность времени;

Δ x – неопределенность координаты.

· Если потенциальное поле U не зависит от времени, то можно записать стационарные уравнения Шредингера. Для одномерного случая уравнения будут иметь вид:

(3.12)

(3.13)

где Е – энергия частицы;

ψ – функция, зависящая от х;

φ – функция, зависящая от t.

Волновая функция частицы

(3.14)

определяется решениями (3.12) и (3.13).

· Для свободного электрона выражение (3.14) прнимает плоской волны, движущейся в направлении х:

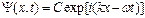, (3.15)

где kx - ωt – фаза волны.

· Участок волны, имеющий данное значение фазы и движущийся в вдоль оси х имеет фазовую скорость:

(3.16)

· В реальном случае волны де Бройля накладываются друг на друга, образуя волновой пакет, который движется с групповой скоростью υ_r:

(3.17)

Эта скорость совпадает со скоростью распространения частицы.

· Вероятность dW обнаружить частицу в интервале dx (для одномерного случая) выражается формулой:

. (3.18)

Вероятность W обнаружить частицу в интервале от x ₁ до x ₂ находится интегрированием:

(3.19)

Собственное значение энергии E_n частицы, находящейся на n- ом энергетическом уровне в бесконечно глубокой потенциальной яме, выражается формулой:

, (3.20)

где L – ширина потенциальной ямы.

Собственная волновая функция, соответствующая (3.20) имеет вид:

. (3.21)

· Коэффициент преломления n волн де Бройля на границе потенциальной ступени, если (низкая потенциальная ступень) имеет вид:

. (3.22)

Коэффициенты отражения R и прохождения А волн де Бройля через низкую потенциальную ступень (рис. 3.2):

(3.23)

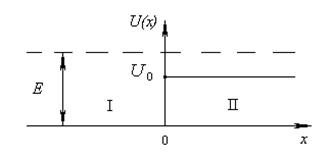
Рис. 3.2

· Коэффициент прозрачности D прямоугольного потенциального барьера ширины d (рис. 3.3)

(3.24)

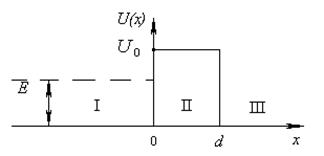
Рис. 3.3

· Собственное значение энергии электрона в водородоподобном атоме:

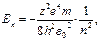(3.25)

где n – главное квантовое число (n=1,2,3,...);

ε₀ – электрическая постоянная;

z –число протонов в ядре атома.

· Квантовый гармонический осциллятор имеет энергию:

Е_п = hν (n +1/2), (3.26)

где n – квантовое число.

· Энергия фонона также определяется формулой

Е_ф = hν. (3.27)

Дата добавления: 2017-02-01