Основные положения теории Максвелла

Лекция 7. Теория Максвелла

Основные положения теории Максвелла. Вихревое электрическое поле. Представление ЭДС индукции с помощью теоремы Стокса. Представление циркуляции вектора напряженности магнитного поля с помощью теоремы Стокса. Ток смещения. Система уравнений Максвелла. Материальные уравнения. Электромагнитные волны. Волновое уравнение. Основные свойства, получение и распространение электромагнитных волн. Энергия электромагнитной (световой) волны. Вектор Умова-Пойтинга. Источники электромагнитного излучения.

Между электрическим и магнитным полями, как уже отмечалось, существует глубокая внутренняя связь, заключающаяся в том, что эти поля могут превращаться друг в друга. Всякое изменение магнитного поля сопровождается появлением электрического поля и, наоборот, всякое изменение электрического поля приводит к появлению магнитного поля. В результате образуется электромагнитная волна. Это взаимное превращение электрического и магнитного полей было открыто в начале второй половины XIX в. Максвеллом, который развил общую теорию электромагнитного поля в покоящихся средах. Теория Максвелла позволяет с единой точки зрения рассмотреть всю совокупность свойств электрических и магнитных полей.

Надо отметить, что возникшее при изменении магнитного поля электрическое поле существенно отличается от электростатического поля. Известно, что силовые линии электростатического поля всегда разомкнуты; они начинаются и заканчиваются на электрических зарядах, и в соответствии с этим напряжение по замкнутому контуру в электростатическом поле всегда равно нулю. По этой причине электростатическое поле не может поддерживать замкнутое движение зарядов и, следовательно, не может привести к возникновению электродвижущей силы.

Электрическое поле, возникающее в проводнике при изменении магнитного потока, связанного с ним (в результате электромагнитной индукции), не связано непосредственно с электрическими зарядами. Линии напряженности такого поля представляют собой замкнутые кривые (подобно линиям индукции магнитного поля). Поэтому его называют вихревым электрическим полем (рис. 7.1). Такое поле порождает 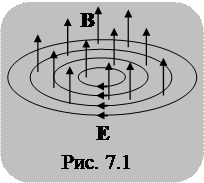в проводниках движение электрических зарядов по замкнутым траекториям и приводит к возникновению электродвижущей силы; при этом сторонними силами являются силы вихревого электрического поля. На рис. 7.1. показанное направление вектора E соответствует возрастанию вектора B. Электрическое напряжение по замкнутому контуру в этом поле не равно нулю; его значение между двумя какими-либо точками не определяется только положением этих точек, как это было отмечено в случае электростатического поля, но зависит от формы проводника (контура), соединяющего данные точки.

Таким образом, анализ явления электромагнитной индукции приводит к следующему выводу, выражающему первое основное положение теории Максвелла: переменные электрическое и магнитное поля не могут существовать отдельно, независимо друг от друга; одно поле порождает другое. Они существуют всегда вместе в виде единого электромагнитного поля, которое в каждой точке пространства характеризуется векторами E и H. Или всякое изменение магнитного поля вызывает появление вихревого электрического поля.

Работа вихревого электрического поля по перемещению положительного единичного заряда вдоль замкнутого неподвижного проводника численно равна ЭДС индукции в этом проводнике.

Формально можно допустить, что заряды непрерывно распределены в какой-то части пространства (хотя на самом деле заряды дискретны, и речь может идти лишь о достаточно большой густоте их распределения). Тогда заряд, заключенный внутри некоторого объема , находится путем интегрирования:

. (7.1)

Предположив, что заряды могут распределяться в пространстве с различной объемной плотностью, теорему Остроградского-Гаусса можно представить в интегральной форме:

. (7.2)

Уравнение (7.2) является одним из уравнений Максвелла в интегральной форме.

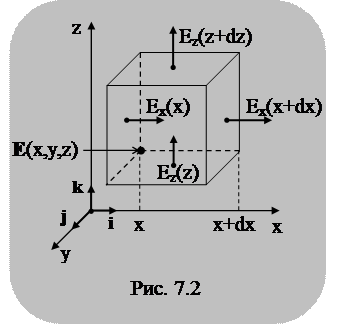Любое реальное электрическое поле в той или иной степени является неоднородным. Для аналитического описания неоднородного поля введем прямоугольную систему координат (рис. 7.2).

Выделим элементарный прямоугольный параллелепипед со сторонами .

Будем считать, что напряжённость в пределах элементарного объёма изменяется по линейному закону.

Так, если в точке с координатами , ,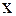

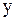, (7.3)

то в точке с координатами , ,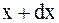

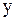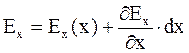. (7.4)

Соответственно в точках 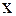, , 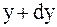и 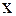, , 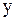будем иметь

(7.5)

и

. (7.6)

Грани параллелепипеда столь малы, что в пределах их поверхности нормальные к ним составляющие 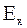, , 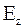остаются постоянными. При таких условиях через грани параллелепипеда проходят потоки вектора :

; ;

; ;

; .

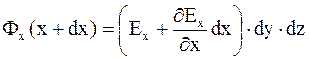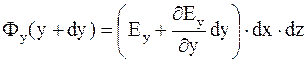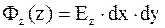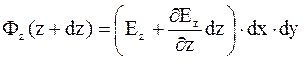Соответственно приращение потока в направлении , ,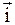

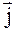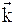
; (7.7)

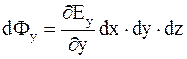; (7.8)

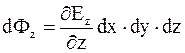. (7.9)

Тогда приращение потока вектора напряженности электрического поля в пределах элементарного объёма

. (7.10)

Выражение в скобках может быть записано с помощью известного оператора 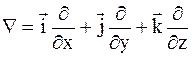и вектора в виде скалярного произведение двух векторов и :

.

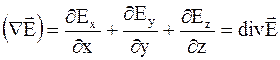В этом случае выражение (2.25) будет иметь вид

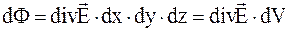. (7.11)

Из выражения (7.11) следует, что полный поток линий напряженности электрического поля через произвольную замкнутую поверхность, охватывающую объем , может быть получен путем интегрирования:

.

Воспользовавшись теоремой Остроградского-Гаусса, будем имть

. (7.12)

Из формулы (7.12) следует

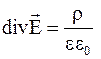. (7.13)

Полученное соотношение (7.13) является одним из уравнений Максвелла в дифференциальной форме.

7.2. Представление ЭДС индукции с помощью теоремы Стокса

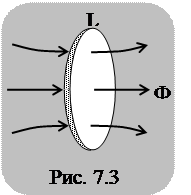Возникновение индукционного тока в контуре свидетельствует о том, что при изменении магнитного потока через поверхность, ограниченную контуром (рис. 7.3), возникают сторонние силы и электроны движутся в поле с напряженностью . При этом ЭДС электромагнитной индукции

.

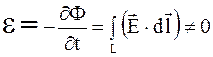Известно, что теорема Стокса позволяет, выразить криволинейный интеграл через поверхностный интеграл. Если - поверхность, ограниченная замкнутым контуром , и рассматриваемый вектор является функцией трех переменных x, y, z (рис. 7.4), то имеет место утверждение: циркуляция вектора напряженности электрического поля по замкнутому контуру равна потоку ротации через любую поверхность , ограниченную контуром . Математически это утверждение можно записать так:

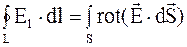. (7.14)

Для рассматриваемого случая имеем

(7.15).

Следовательно,

.

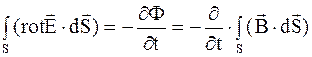Откуда

. (7.16).

Полученное математическое выражение закона электромагнитной индукции (7.16) известно как одно из уравнений Максвелла в дифференциальной форме.

Дата добавления: 2017-02-01