Система уравнений Максвелла

Ток смещения

Представление циркуляции с помощью теоремы Стокса

С помощью теоремы Стокса можно преобразовать теорему о циркуляции вектора напряженности магнитного поля .

Известно, что математически теорема о циркуляции вектора напряженности магнитного поля может быть записана так:

или

. (7.17)

С помощью теоремы Стокса получаем

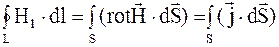. (7.18)

Из выражения (7.18) находим

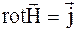, (7.19)

где - плотность тока.

Формула (7.19) представляет математическое выражение теоремы о циркуляции 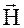в дифференциальной форме.

Надо отметить, что полученные соотношения (7.16) и (7.19) справедливы только для стационарных процессов (для постоянного тока).

Для нестационарных процессов, когда токи зависимы от времени, эти формулы неверны. Для доказательства этого утверждения выполним операцию дивергенции от обеих частей равенства (7.19):

или

.

Так как с математической точки зрения , то , что выполняется только в случае постоянного тока, т.к. из уравнения непрерывности для тока только для постоянного тока, когда

.

Если же ток переменный, то объемная плотность заряда в отдельных точках цепи является переменной величиной, следовательно,

.

Смысл уравнения основного закона электромагнитной индукции

заключается в том, что изменяющееся магнитное поле создает вихревое электрическое поле, последнее в свою очередь вызывает в окружающем пространстве (веществе или вакууме) изменяющееся магнитное поле. Поскольку магнитное поле создается электрическим током, то вихревое электрическое поле следует рассматривать как некоторый ток, который протекает как в веществе, так и в вакууме. Максвелл назвал этот ток током смещения.

Таким образом, ток смещения – это изменяющееся со временем электрическое поле (вихревое электрическое поле), которое порождает магнитное поле так же, как и ток проводимости.

Механизм тока смещения можно установить, рассмотрев один из опытов А.А. Эйхенвальда. В этом опыте (рис. 7.5) диэлектрический диск Д вращается между четырьмя неподвижными заряженными полудисками А, А₁, В, В₁. При прохождении точками диска Д плоскости «ав», перпендикулярной чертежу и разделяющей заряженные полудиски, меняется направление электрического поля (знак поля), действующего на диэлектрик. В результате чего происходит изменение знака поляризационных зарядов диэлектрика. Если вращение диска происходит, так как показано на рис. 7.5, то на левой стороне диска вместо положительных зарядов при переходе через плоскость «ав» появляются отрицательные заряды, а на правой стороне вместо отрицательных зарядов появляются положительные заряды. Это означает, что в движущемся диске в плоскости «ав» происходит как бы движение зарядов: слева направо положительных, а справа налево отрицательных. Эти движения зарядов, представляющие собой смещение зарядов в молекулах диэлектрика, образуют ток смещения в диэлектрике, текущий слева направо. Эйхенвальд установил, что токи смещения (как и конвекционные токи) создают магнитное поле.

Токи смещения наблюдаются в конденсаторах, включенных в цепь переменного тока (рис. 7.6). Известно, что для постоянного тока конденсатор, включенный в цепь последовательно, является бесконечно большим сопротивлением, если его диэлектрик не обладает утечкой. В такой цепи лишь в момент ее замыкания протекает импульс зарядного тока, соответствующий небольшому смещению электронов проводимости. Если в цепи с конденсатором существует источник переменного тока, то в такой цепи за каждый период протекают токи заряда и разряда конденсатора. Сопротивление конденсатора при этом не бесконечно велико, а зависит от емкости конденсатора и частоты тока:

.

В этом случае конденсатор необходимо рассматривать не как разрыв цепи, а как участок цепи с другим механизмом проводимости. Если между обкладками конденсатора находится полярный или поляризующийся в электрическом поле диэлектрик, то при приложении разности потенциалов к обкладкам конденсатора электрические заряды смещаются вдоль линий напряженности электрического поля. Это смещение зарядов (ионов) образует ток смещения в диэлектрике. Ток смещения существует не только в диэлектрике, но и в вакууме, где он представляет собой изменение напряженности электрического поля во времени.

Рассмотрим процессы, протекающие в схеме, представленной на рис. 7.6, где источник переменного тока (генератор), напряжение которого U, заряжает и перезаряжает конденсатор емкостью С. Если конденсатор плоский, то его емкость 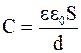, заряд конденсатора 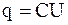. Тогда зарядный ток, который является током смещения, протекающий через конденсатор,

.

Плотность этого тока

.

В векторной форме

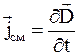, (7.20)

где D – вектор индукции электрического поля.

Так как 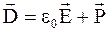, где - вектор поляризации, то плотность тока смещения в диэлектриках

, (7.21)

где - плотность тока смещения в вакууме;

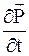- плотность тока поляризации (тока, обусловленного упорядоченным движением электрических зарядов в диэлектрике), который представляет собой смещение зарядов в неполярных молекулах, поворот диполей в полярных молекулах.

Полный ток в проводящей цепи равен сумме тока проводимости (а также конвекционного тока) и тока смещения.

Поэтому плотность полного тока равна

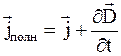, (7.22)

где j – вектор плотности тока проводимости.

Так как ток смещения определяется производной 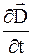, а не самой величиной вектора индукции электрического поля, то при убывании поля (например, внутри конденсатора, обладающего проводимостью при его разрядке) производная отрицательна. Ток смещения направлен от минуса к плюсу, в то время как ток проводимости всегда направлен от плюса к минусу, поэтому полный ток будет равен

.

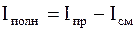При равенстве токов смещения и проводимости полный ток может быть равен нулю.

С учетом того что для полного тока , имеем

, (7.23)

где 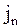- проекция вектора плотности тока проводимости на направление положительной нормали к выбранной поверхности S;

- проекция вектора плотности индукции вихревого электрического поля на направление положительной нормали к выбранной поверхности S.

Уравнение (7.23) представляет собой обобщение закона полного тока на случай любых токов и выражает одно из основных положений теории Максвелла: токи смещения (а также конвекционные токи) создают такие же магнитные поля, как и токи проводимости.

Уравнения Максвелла являются фундаментальными уравнениями классической макроскопической электродинамики, описывающими электромагнитные явления в любой среде и в вакууме. Они сформулированы Дж. Максвеллом в 60-х годах XIX века на основе обобщения эмпирических законов электрических и магнитных явлений и развития идеи М. Фарадея о том, что взаимодействия между электрически заряженными телами осуществляются посредством электромагнитного поля. Они связывают величины, характеризующие электромагнитное поле, с его источниками, т. е. с распределением в пространстве электрических зарядов и токов.

В вакууме электромагнитное поле характеризуется напряженностью электрического поля E и вектором магнитной индукции B, зависящими от пространственных координат и времени. Эти величины определяют силы, действующие со стороны поля на заряды и токи, распределение которых в пространстве задается объемной плотностью заряда r и плотностью электрического тока j. Для описания электромагнитных процессов в материальной среде, кроме векторов E и B, вводятся вспомогательные векторные величины, зависящие от состояния и свойств среды: индукция электрического поля D и напряженность магнитного поля H.

Уравнения Максвелла позволяют определить основные характеристики электромагнитного поля (E, B, D и H) в каждой точке пространства в любой момент времени, если известны плотность тока и объемная плотность заряда как функции координат и времени. Они могут быть записаны в интегральной или дифференциальной форме.

7.5.1. Система уравнений Максвелла в интегральной форме

Уравнения Максвелла в интегральной форме определяют не векторы E, B, D и H в отдельных точках пространства, а некоторые интегральные величины, зависящие от распределения этих характеристик поля: циркуляцию векторов E и H вдоль произвольных замкнутых контуров и потоки векторов B и D через произвольные замкнутые поверхности.

1. Первое уравнение является обобщением на переменные электромагнитные поля эмпирического закона Био-Савара-Лапласа о возбуждении магнитного поля электрическими токами. Оно показывает, что источниками магнитного поля могут быть не только движущиеся в проводниках электрические заряды (электрические токи), но и изменяющиеся во времени электрические поля в диэлектриках или вакууме. Величина, пропорциональная скорости изменения электрического поля во времени, была названа Максвеллом током смещения, который возбуждает магнитное поле по тому же закону, что и ток проводимости. Полный ток, равный сумме тока проводимости и тока смещения, всегда является замкнутым. Первое уравнение Максвелла свидетельствует о том, что циркуляция вектора напряженности магнитного поля вдоль замкнутого контура L определяется полным током через произвольную поверхность S, ограниченную данным контуром. Первое уравнение Максвелла имеет вид

, (7.24)

где 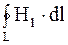- циркуляция вектора напряженности магнитного поля;

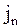- проекция вектора плотности тока на направление положительной нормали к бесконечно малой площадке dS, являющейся частью поверхности S;

- проекция вектора плотности тока смещения на ту же нормаль.

2. Второе уравнение является математической формулировкой закона электромагнитной индукции и записывается в виде

, (7.25)

где - циркуляция вектора напряженности результирующего поля, потенциального и вихревого;

B_n – проекция вектора индукции магнитного поля на направление положительной нормали к бесконечно малой площадке dS, являющейся частью поверхности S;

Знак «минус» – соответствует закону (правилу) Ленца для определения направления индукционного тока.

Уравнение (7.25) утверждает, что циркуляция вектора напряженности результирующего электрического поля вдоль замкнутого контура L (ЭДС индукции) определяется скоростью изменения потока вектора магнитной индукции через поверхность S, ограниченную замкнутым контуром L.

3. Третье уравнение отражает то свойство вектора B, что его линии замкнуты или уходят в бесконечность (теорема Остроградского-Гаусса для магнитного поля). Это уравнение отображает опытные данные об отсутствии магнитных зарядов, аналогичных электрическим зарядам. Магнитное поле порождается только электрическим током. Математически его можно записать так:

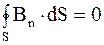. (7.26)

Таким образом, поток вектора магнитной индукции через произвольную замкнутую поверхность S равен нулю.

4. Четвертое уравнение показывает, что линии вектора D могут начинаться и оканчиваться на зарядах (теорема Остроградского-Гаусса для вектора D). Данное уравнение представляет собой обобщение закона взаимодействия неподвижных электрических зарядов (закона Кулона):

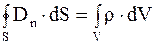. (7.27)

Поток вектора индукции электрического поля через произвольную замкнутую поверхность S определяется электрическим зарядом, находящимся внутри этой поверхности (в объеме V, ограниченном поверхностью S).

7.5.2. Система уравнений Максвелла в дифференциальной форме

Если считать, что векторы электромагнитного поля E, B, D и H являются непрерывными функциями координат, то, рассматривая циркуляцию E и H по бесконечно малым контурам и потоки векторов B и D через поверхности, ограничивающие бесконечно малые объемы, можно от системы уравнений Максвелла в интегральной форме перейти к системе уравнений Максвелла в дифференциальной форме, характеризующих поле в каждой точке пространства:

1) ; (7.28)

2) 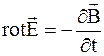; (7.29)

3) ; (7.30)

4) 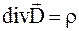. (7.31)

Физический смысл уравнений Максвелла в дифференциальной форме аналогичен физическому смыслу этих уравнений в интегральной форме.

7.5.3. Материальные уравнения

Уравнения Максвелла в интегральной и дифференциальной формах не образуют полной замкнутой системы, позволяющей рассчитывать электромагнитные процессы при наличии материальной среды. Поэтому систему уравнений Максвелла необходимо дополнить соотношениями, связывающими векторы E, B, D, H и j, которые являются независимыми. Связь между ними определяется свойствами среды и ее состоянием, причем векторы D и j выражаются через вектор E, а B – через H. Эти уравнения называются уравнениями состояния или материальными уравнениями. Они описывают электромагнитные свойства среды и для каждой конкретной среды имеют определенную форму. Для большинства изотропных сред, вплоть до значительных полей, уравнения состояния (материальные уравнения) имеют простую линейную связь:

1. Первое уравнение связывает векторы напряженности и индукции электрического поля:

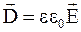, (7.32)

где e(x,y,z) –диэлектрическая проницаемость среды;

e₀ – диэлектрическая постоянная.

2. Второе уравнениесвязывает векторы индукции и напряженности магнитного поля:

, (7.33)

где m (x,y,z) – магнитная проницаемость среды;

m₀ – магнитная постоянная.

3. Третье уравнение выражает закон Ома в дифференциальной форме

, (7.34)

где g - удельная электропроводность;

j _стр. – плотность так называемых сторонних токов, т.е. токов, поддерживаемых любыми силами, кроме сил электрического поля (например, магнитным полем, диффузией).

Проницаемости e и m определяют тот вклад в электромагнитное поле, который вносят связанные заряды, входящие в состав электрически нейтральных атомов и молекул вещества. Объемная плотность заряда r и плотность тока j в материальных уравнениях – это плотности свободных зарядов и токов, причем вспомогательные векторы D и H, вводятся так, чтобы циркуляция вектора H определялась только движением свободных зарядов, а поток вектора D – плотностью распределения этих зарядов в пространстве. Материальные уравнения используются при решении уравнений Максвелла.

Из уравнений Максвелла вытекает ряд законов сохранения: закон сохранения электрического заряда, закон сохранения электромагнитной энергии. В частности, из уравнений и 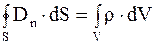можно получить уравнение непрерывности, представляющее собой закон сохранения электрического заряда: полный ток, протекающий за единицу времени через любую замкнутую поверхность S, равен изменению заряда внутри объема V, ограниченного поверхностью S. Если ток через поверхность отсутствует, то заряд в объеме V остается неизменным:

. (7.35)

Если энергия электромагнитного поля не переходит в другие виды энергии, то, согласно уравнениям Максвелла, изменение энергии в некотором объеме за единицу времени равно потоку электромагнитной энергии через поверхность, ограничивающую этот объем.

Если внутри объема за счет энергии электромагнитного поля выделяется некоторое количество тепла, то закон сохранения энергии утверждает о том, что изменение энергии электромагнитного поля в некотором объеме V равно сумме потока энергии электромагнитного поля и количества теплоты, выделившейся в этом объеме:

, (7.36)

где w – энергия поля в единице объема;

П_n – проекция вектора Умова-Пойтинга на направление положительной нормали к поверхности dS;

Q – количество тепла, выделяемое в единицу времени.

Уравнения Максвелла приводят к фундаментальному выводу о конечности скорости распространения электромагнитных взаимодействий. Это означает, что при изменении плотности заряда или тока, порождающих электромагнитное поле, в некоторой точке пространства на расстоянии r от них поле изменится спустя время . Вследствие конечной скорости распространения электромагнитных взаимодействий, следовательно, возможно существование электромагнитных волн, частным случаем которых является свет, что было впервые доказано Максвеллом.

Это заключение называют вторым основным положением теории Максвелла: электромагнитное поле, возникнув в одном месте пространства, не остается локализованным в нем, а распространяется от этого места в виде электромагнитной волны. Векторы E и H электромагнитной волны взаимно перпендикулярны и перпендикулярны вектору скорости v, с которой распространяется электромагнитная волна.

Дата добавления: 2017-02-01