Метод контурных токов

Метод основан на 2-м законе Кирхгофа. При его использовании в составе анализируемой схемы выбирают независимые контуры и предполагают, что в каждом из контуров течет свой контурный ток. Для каждого из независимых контуров составляют уравнение по 2-му закону Кирхгофа и их решают. Токи в ветвях находят как алгебраическую сумму контурных токов, протекающих по данной ветви.

Все источники сигналов, представленные источниками тока, заменяют источниками ЭДС (рис. 4.29).

Эта схема эквивалентна, если

а) E = I Z _i ^I;

б) Z_i ^II = Z_i ^I.

1) Топологический анализ схемы.

а) Как и в предыдущем методе, определяют число ветвей b.

б) Определяют число узлов у.

в) Подсчитывают число независимых контуров N_k = b – y + 1.

Все независимые контуры обозначены дугами со стрелками на них, которые показывают положительное направление обхода.

Все контуры нумеруют и каждому контуру присваивают свой контурный ток: I_{k 1}; I_{k 2}; I_kNk.

За положительное направление контурного тока принимают положительное направление обхода контура.

2) По второму закону Кирхгофа относительно контурных токов записывают уравнения, которые после приведения подобных членов образуют систему линейных уравнений N_k = N_k порядка:

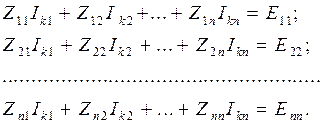
где I_ki – контурный ток i -го контура;

Z_ii – собственное сопротивление i -го контура и равно алгебраической сумме сопротивлений, входящих в i -й контур;

Z_ji – сопротивление смежных ветвей между i -м и j -м контурами. Оно представляет собой алгебраическую сумму, причем ее члены берутся со знаком «+», если контурные токи направлены одинаково, и со знаком «–», если они направлены встречно;

E_ki – контурная ЭДС i -ого контура. Она равна алгебраической сумме ЭДС, входящих в i -й контур. Контурная ЭДС E_ki берется со знаком «+», когда направление источника ЭДС и направление тока совпадают, и со знаком «–», если они направлены встречно.

3) По правилу Крамера находят контурные токи I_ki= .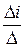

4) Токи в ветвях находят как алгебраическую сумму контурных токов, протекающих через данную ветвь. В алгебраической сумме контурные токи берутся со знаком «+», если ток ветви и совпадает с контурным током и «–» если не совпадает.

Если токи ветви оказались положительными, то выбранное направление тока совпадает с истинным и наоборот.

Пример. Дана комплексная схема замещения электрической цепи (рис. 4.30). Определить токи во всех ветвях.

1. Проводим топологический анализ

а) b = 6; б) y = 4; в) N_k = 6 – 4 + 1=3.

2) Составим систему уравнений по методу МКТ

где:

E ₁₁ = E ₁; E ₂₂ = 0; E ₃₃ = 0.

3) По методу Крамера находим контурные токи I_ki = .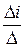

4) Находим токи в ветвях: I ₁ = I_{k 1}; I ₂ =
= I_{k 1} – I_{k 2}; I ₃ = I_{k 1} – I_{k 3}; I ₄ = – I_{k 2} + I_{k 3}; I ₅ = I_{k 2}; I ₆ = I_{k 3}.

Пример 2. Пример расчета по заданию №1

На рис. 1 приведена исходная схема замещения цепи постоянного тока, параметры которой заданы

Рис. 1.

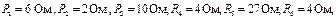
1. Выполнение первого пункта задания [1, 2, 5, 6].

1.1. Проводим эквивалентные преобразования с целью упрощения расчетов. Объединяем последовательно соединенные -элементы (рис. 2)

1.2. Произвольно задаем положительные направления токов в ветвях схемы (рис.2).

Рис. 2.

1.3. Составляем часть уравнений расчетной системы, используя только первый закон Кирхгофа. Выбираем 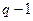узлов на схеме (данная схема содержит узла, которые отмечены арабскими цифрами) и для каждого из них составляем уравнение по первому закону Кирхгофа

1.4. Всего необходимо составить 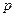уравнений в расчетной системе ( 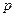- число неизвестных токов, равное числу ветвей на схеме). Поэтому число уравнений, которое необходимо составить, используя второй закон Кирхгофа, равно 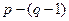(для данной схемы и ).

1.4.1. Выбираем 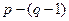независимых контуров на схеме, в каждом из них произвольно задаем направление обхода контура (отмечено круглыми стрелками на рис.2).

1.4.2. Для каждого из выбранных контуров составляем уравнение, используя второй закон Кирхгофа, а также закон Ома ()

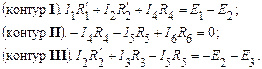
1.5. Полученные уравнения объединяем в систему, которую упорядочиваем

и представляем в матричной форме записи, подставив численные значения параметров схемы

.

Первый пункт задания выполнен.

2. Выполнение второго пункта задания [1, 2, 5, 6].

2.1. Используя эквивалентно преобразованную схему (рис.2), произвольно задаем положительное направление токов в каждой ветви схемы (рис.3) (в данном примере они оставлены без изменения).

2.2. Выбираем независимых контуров на схеме, в каждом из них произвольно задаем направление контурного тока 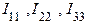(отмечено круглыми стрелками на рис.3).

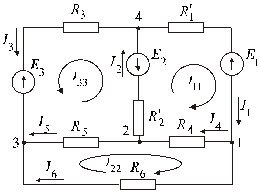
Рис. 3.

2.3. Определяем составляющие системы контурных уравнений:

·собственные сопротивления контуров

; ; ;

·общие сопротивления между контурами

Ом; Ом; Ом;

·контурные ЭДС, действующие в выбранных контурах

В.

Знаки слагаемых при определении контурных ЭДС определяются совпадением (+) или несовпадением (–) положительного направления ЭДС источника, входящего в рассматриваемый контур, с направлением контурного тока этого же контура.

2.4. Составляем систему контурных уравнений. При этом используем для каждого контура второй закон Кирхгофа и принцип наложения (суперпозиции)

На первом месте в левой части уравнений стоят составляющие полного напряжения в контуре, представляющие собой частичное напряжение, вызванное протеканием в рассматриваемом контуре собственного контурного тока. Знак этих слагаемых всегда положителен (+) (условно это можно обосновать тем, что контурный ток рассматриваемого контура «сам с собой всегда совпадает»). Остальные слагаемые представляют собой частичные напряжения, вызванные протеканием контурных токов смежных контуров на общих ветвях с рассматриваемым контуром. Знак этих слагаемых определяется совпадением (+) или несовпадением (–) контурных токов смежных контуров на их общих ветвях.

2.5. Полученную систему упорядочиваем

и представляем в матричной форме записи, подставив численные значения составляющих системы контурных уравнений

.

2.6. Решаем полученную систему контурных уравнений, используя правило Крамера [1]:

2.6.1. Вычисляем главный определитель системы, разворачивая квадратную матрицу контурных сопротивлений по первой строке (следует заметить, что величина определителя не зависит от того, по какой строке или столбцу его разворачивают)

2.6.2. Вычисляем дополнительные определители системы, последовательно заменяя столбцы матрицы контурных сопротивлений матрицей-столбцом контурных ЭДС. Каждый дополнительный определитель рассчитываем, разворачивая его по первой строке аналогичным образом

;

;

;

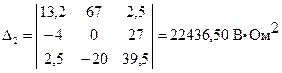2.6.3. Определяем контурные токи

; ; .

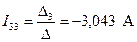2.7. Используя рассчитанные контурные токи, определяем реальные токи в ветвях схемы. Руководствуемся правилом: реальные токи в независимых ветвях схемы (принадлежащих только одному контуру) определяются только контурным током рассматриваемого контура

.

Реальные токи в общих ветвях между смежными контурами определяются по принципу наложения: алгебраической суммой смежных контурных токов. При этом знак каждого контурного тока определяется совпадением (+) или несовпадением (–) его направления с заданным положительным направлением реального тока в рассматриваемой ветви.

.

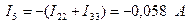Второй пункт задания выполнен.

3. Выполнение третьего пункта задания [1, 2, 5, 6].

Рассматриваемая схема замещения содержит четыре узла, поэтому к заданной схеме метод двух узлов непосредственно не применим.

3.1. Используя эквивалентное преобразование участка схемы , соединенного по схеме «треугольник», в участок , соединенный по схеме «звезда» (отмечен на рис. 4 пунктиром), приводим начальную схему к схеме, содержащей два узла (рис.5).

Рис. 4. Рис. 5.

При этом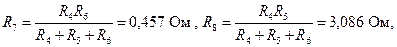

.

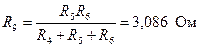Эквивалентно объединяя последовательно соединенные -элементы в каждой ветви, получаем исходную схему для расчета методом двух узлов (рис. 6).

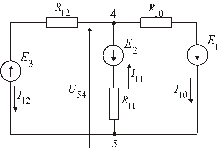
Рис. 6.

При этом

3.2. Произвольно задаем положительное направление токов в ветвях схемы и положительное направление узлового напряжения (рис. 6).

3.3. Рассчитываем проводимости ветвей схемы

.

3.4. Используя основную формулу метода, определяем узловое напряжение :

.

Знак слагаемых числителя определяется несовпадением (+) или совпадением (–) положительного направления и положительного направления ЭДС рассматриваемой ветви.

3.5. Рассчитываем неизвестные токи в ветвях, используя обобщенный закон Ома

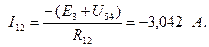
Проанализируем результаты расчета. На рис. 5 в каждой ветви источник ЭДС и -элементы соединены последовательно. Поэтому токи в этих ветвях равны рассчитанным. Однако участки схемы в окрестности источников не были охвачены преобразованием. Следовательно, в соответствии с условием эквивалентности преобразования участков схем величина этих токов должна остаться такой же, как и до преобразования. Сравниваем по модулю значения токов, рассчитанных настоящим методом и методом контурных токов

Видно, что значения токов практически совпадают. Следовательно, оба расчета проведены корректно. Третий пункт задания выполнен.

4. Выполнение четвертого пункта задания [1, 2, 5, 6].

4.1. Разрываем шестую ветвь и произвольно задаем положительное направление токов в остальных ветвях, положительное направление напряжения холостого хода и напряжения между узлами и (рис. 7).

Рис.7.

4.2. Определяем величину . Для этого предварительно рассчитываем методом двух узлов.

.

.

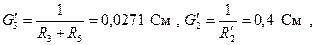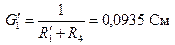Используя основную формулу метода, определяем узловое напряжение

.

Рассчитываем токи и , и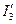спользуя обобщенный закон Ома

Для контура, включающего , составляем уравнение по второму закону Кирхгофа (направление обхода контура указано круглой стрелкой) и рассчитываем

,

.

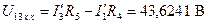4.3. Определяем входное сопротивление схемы со стороны зажимов разомкнутой ветви . Для этого эквивалентно преобразуем участок схемы , соединенный звездой, в участок, соединенный треугольником .

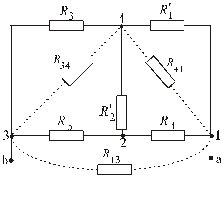
Рис. 8.

Преобразованная схема будет иметь вид (рис. 9)

Рис. 9.

.

Используя свойства параллельного последовательного соединения 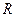- элементов, определяем

;

.

4.4. Определяем искомый ток, используя закон Ома для замкнутой цепи

.

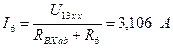Аналогичный ток, рассчитанный методом контурных токов, составляет

.

Они практически совпадают. Расчет проведен верно. Четвертый пункт задания выполнен.

5. Выполнение пятого пункта задания [1, 2, 5, 6]

Составим уравнение баланса мощностей для преобразованной схемы (рис. 2) с учетом выбранного на ней положительного направления токов.

5.1. Определяем режим работы каждого активного элемента, руководствуясь правилом. Если истинное положительное направление тока, протекающего через источник ЭДС (которое можно определить только в результате расчета), совпадает с положительным направлением ЭДС этого источника, то активный элемент работает в режиме генератора. В противном случае он работает в режиме приемника.

Сопоставляя на рис. 2 заданное положительное направление токов, знаки рассчитанных токов и положительное направление ЭДС активных элементов, определяем их режим работы:

источник ЭДС - генератор, ;

источник ЭДС - приемник, ;

источник ЭДС - генератор, .

5.2. Составляем и численно проверяем корректность уравнения баланса мощностей (значения токов берем посчитанными методом контурных токов; мощность на пассивных приемниках определяем по закону Джоуля – Ленца)

,

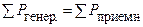где

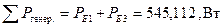
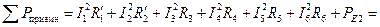
= 545,124 Вт.

Видно, что значения суммарных мощностей практически совпадают. В то же время на примере баланса мощностей покажем проверку корректности расчета любого параметра, указанного в задании. Воспользуемся абсолютным значением относительной погрешности

Расчет считается корректным, если . Итак пятый пункт задания и все задание выполнены.

Метод узловых потенциалов (МУП)

Метод основан на применении первого закона Кирхгофа. В нем за неизвестные величины принимают потенциалы узлов. По закону Ома определяют токи во всех ветвях схемы.

Все источники ЭДС, имеющиеся в схеме, заменяют источниками тока (рис. 4.31).

а) I = E / Z_i ^I;

б) Z_i ^II = Z_i ^I.

1) Топологический анализ.

а) Подсчитывают число ветвей b и число узлов y. Определяется количество независимых узлов N_y = y – 1.

б) Нумеруют все узлы. Один из узлов, к которому сходится наибольшее число ветвей, считают нулевым, где – потенциал нулевого узла.

2) По 1-му закону Кирхгофа составляют уравнения для N узлов схемы и решают их относительно потенциалов узлов:

,

где Y_ii – собственная узловая проводимость. Она равна сумме проводимостей всех ветвей, сходящихся в i -м узле, все они берутся со знаком «+»;

Y_ij – межузловая проводимость между i -м и j -м узлами. Проводимости всех узлов берутся со знаком «–»;

I_ii – алгебраическая сумма токов источников тока, сходящихся в i -м узле. Втекающие токи записываются в эту сумму со знаком «+», а вытекающие – со знаком «–».

3) Потенциалы узлов находят по формуле Крамера

.

4) Токи в ветвях находят по закону Ома

I = (j₁ – j₂)/ Z.

Пример. Дана электрическая цепь (рис. 4.32). Рассчитать токи во всех ветвях.

Z ₂

I ₂

Предварительно преобразуем все источники напряжения (рис. 4.32) в источники тока (рис. 4.33).

Z ₄

Z ₃

Z ₁

I ₁

I ₃

I

I

I ₄

I ₂

I ₁

E ₂

E ₁

Z ₄

Z ₃

Z ₂

Z ₁

Рис. 4.32 Рис. 4.33

Проведем топологический анализ.

а) число ветвей b = 4;

б) число независимых узлов N_у = 2, их потенциалы: φ₁ и φ₂ (рис. 4.33).

Составим систему уравнений по методу узловых потенциалов:

;

.

По методу Крамера найдем потенциалы узлов .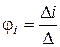

По закону Ома найдем токи во всех ветвях схемы:

.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЗАДАНИЙ по теме "цепи переменного тока"

Дата добавления: 2017-02-01