Где EA, EB, EC – комплексные напряжения источника питания.

Ya = 1/Za; Yb = 1/Zb; Yc= 1/Zc – комплексные проводимости фаз приемника.

Комплексный ток в нейтральном проводе находят в соответствии с уравнением, составленным по первому закону Кирхгофа для нейтральной

....

точки n цепи: I_N =Ia + Ib + Ic.

Комплексные фазные напряжения приёмника электроэнергии находят из уравнений, составленных по второму закону Кирхгофа для замкнутого контура:

.........

Ua=E_A- UnN; Ub=E_B - UnN; Uc=E_C - UnN.

При этом фазные токи приёмника определяют по закону Ома для соответствующих участков цепи:

......

Ia=Ua/Za; Ib=Ub/Zb; Ic=Uc/Zc.

Трёхфазная система обеспечивает приёмники электроэнергии симметричным питанием. При этом активная, реактивная и полная мощности могут быть определены по следующим формулам с учётом знака реактивных сопротивлений:

P = I²_A Ra + I²_B Rb + I²_C Rc =UaIa cosΨa + UbIb cosΨb + UcIc cosΨc;

Q= I²_A Xa + I²_B Xb + I²_C Xc = IaUa sinΨa + IbUb sinΨb + IcUc sinΨc;

S = = I²_A Za + I²_B Zb + I²_C Zc;

где cosΨa = Ra/ Za; cosΨb = Rb/ Zb; cosΨc = Rc/ Zc;

sinΨa = Xa/ Za; sinΨb = Xb/ Zb; sinΨb = Xb/ Zb.

При симметричной нагрузке эти формулы приводят к виду:

P= 3 Iф²Rф= 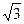Uл Iл cosΨф;

Q= 3 Iф²Xф= 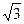Uл Iл sinΨф;

S= = 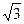Uл Iл,

где cosΨф = Rф/ Zф; sinΨф = Xф/ Zф.

4.1Трёхфазные электрические цепи при соединении фаз приёмника “треугольником”.

В связанных трёхфазных системах наряду с соединением трёхфазных потребителей “звездой” применяется соединение фаз “треугольником”. При этом не имеет значения как соединены фазы источника - “звездой ” или “треугольником”.

При соединении “треугольником” фазные напряжения оказываются равными линейным напряжениям:

(Uф=Uл): Uab=U_AB; Ubc=U_BC; Uca=U_СA.

Соотношение между линейными и фазными токами определяют из уравнений, составленных для токов в соответствии с первым законом Кирхгофа для узлов a,b,c разветвления электрической цепи:

I_А = Iab - Ica; I_В = Ibc - Iab; I_С = Ica - Ibc.

При симметричной нагрузке линейные токи I_А= I_В = I_С = I_Л и фазные

Iab = Ibс = Iса = Iф. При этом угол сдвига фаз между фазными токами и напряжениями Ψab= Ψbc= Ψca= Ψф.

В соответствии с этим при симметричной нагрузке имеет место соотношение I_Л = 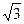Iф.

Пример 1. Заданы эквивалентная схема замещения трехфазного приемника и ее параметры, а также задано линейное напряжение со стороны приемника

Рис. 12.

Выполнить следующие действия:

1. Определить линейные токи, фазные токи и фазные напряжения;

2. Рассчитать активную, реактивную мощность на всем приемнике и на каждой фазе в отдельности;

3. Построить на комплексной плоскости векторную диаграмму токов и напряжений.

Расчет проводим в следующем порядке:

1. Определяем комплексы действующих значений фазных ЭДС

2. Определяем комплексы действующих значений линейных и фазных напряжений

3. Рассчитываем комплексные сопротивления фаз приемника

4. По закону Ома определяем фазные токи

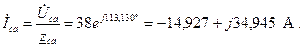
5. Рассчитываем линейные токи, используя первый закон Кирхгофа

6. Определяем полные комплексные, полные активные и реактивные мощности каждой фазы и эти же мощности на всем трехфазном приемнике

При этом

Без специальной проверки видно, что баланс мощностей подтверждается. Следовательно расчеты проведены корректно.

7. Строим векторную диаграмму токов, напряжений и ЭДС. Задаемся масштабами по току и по напряжению:

Рис. 13.

Третий пункт и все задание выполнены.

При выполнении задания №3 можно воспользоваться рекомендуемой литературой [2, 3, 6,7].

Пример 2. Расчет трехфазной цепи с несимметричной нагрузкой (звезда)

К трехфазному источнику подключена цепь (рис. 1). Значения линейного напряжения, активных, индуктивных и емкостных сопротивлений приемников приведены ниже.
Требуется:

1. Определить фазные и линейные токи для заданной схемы соединения, а также ток в нейтральном проводе для схемы «звезда».

2. Определить активную и реактивную мощности, потребляемые цепью.

3. Построить векторную диаграмму напряжений и токов.

Исходные данные:
UЛ = 220 В, XC1 = 10 Ом, R2 = 9 Ом, XL2 = 13 Ом, XL3 = 8 Ом
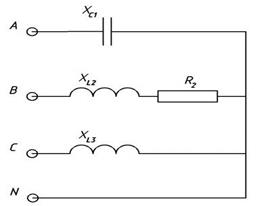Рис. 1

Дата добавления: 2017-02-01