Методические указания к решению задач 3.

В электротехнике простейшим переменным сигналом является гармонический ( ЭДС - е (t), напряжение - (u (t), ток - i (t)).

Применяют несколько способов представления гармонических (синусоидальных – sin или косинусоидальных –cos) электрических величин.

1. Временной (аналитический) способ - ток задается аналитически в виде функции времени (1.1). Аналитически гармонический сигнал (например, напряжение) записывается выражением:

u (t) = U_m sin(ω₀ t+ φ ₀), (1.1 )

где u (t) – мгновенное значение напряжения – напряжение в момент времени t.

Временная диаграмма гармонического сигнала приведена на рис.1.1. Он характеризуется следующими тремя основными параметрами:

1. u_m – амплитуда, величина наибольшего отклонения от нуля, (В- вольт);

2. Т – период, наименьший интервал времени, по истечении которого мгновенные величины повторяются, измеряется в (сек), с ним связаны f=1 / Т – циклическая частота, измеряется в (Гц) и ω₀ =2πf – угловая частота - (рад/с);

3. φ₀ – начальная фаза, (рад). Выражение в скобках - (ω₀ t+ φ₀)=ψ(t) называют полная фаза. Отсюда φ₀ = ψ(t=0).

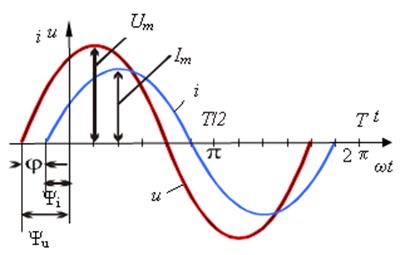
Рис. 1.2. Временные диаграммы двух гармонических сигналов

Кроме амплитуд о величине периодических сигналов судят по их среднеквадратичным (действующим) значениям за период, I, U, E –

, , .

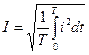Для синусоидальных сигналов законы Кирхгофа и Ома и анализ цепей удобно проводить используя комплексную форму записи.

При комплексном представлении гармоническое колебание как функция времени заменяется комплексной амплитудой, т.е. комплексным числом, не зависящим от времени. Это делается для упрощения записи и выполнения операций над гармоническими функциями.

Комплексная амплитуда содержит информацию о двух важнейших параметрах гармонического сигнала – об амплитуде и начальной фазе. Комплексная амплитуда и гармоническая функция времени при известной частоте ω связаны взаимнооднозначно, т.е.

.

Пример 1. Например, гармоническому колебанию u (t) = 256 cos(2π100 t – 45°) соответствует комплексная амплитуда _m = 256 e^{– j 45}.

Справедливо и обратное. Если известна комплексная амплитуда гармонического сигнала _m = 256 e^{– j 45} и частота ω=2π100, то этому соответствует гармоническое колебание u (t) = 256 cos(2π100 t – 45°).

Геометрически комплексная амплитуда представляет собой вектор, характеризуемый модулем и фазой, равными, соответственно, амплитуде и начальной фазе гармонической функции, как это показано на рис. 4.7,

Законы Ома и Кирхгофа в комплексной форме

Они имеют совершенно такой же вид, как и соответствующие уравнения для цепей постоянного тока. Только токи, ЭДС, напряжения и сопротивления входят в уравнение в виде комплексных величин: комплексных амплитуд и комплексных сопротивлений.

1. Закон Ома. Он устанавливает связь между комплексными амплитудами тока и напряжения на участке цепи. 1.8. Закон Ома для участка цепи, не содержащего источника ЭДС (рис. 1.8):

,

где и - комплексные амплитуды тока и напряжения на участке цепи; Z – комплексное сопротивление участка цепи, 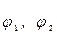–комплексные амплитуды потенциалов на данном участке цепи.

2. Первый закон Кирхгофа: Алгебраическая сумма комплексных амплитуд (действующих значений) токов в узле равна нулю

. (1.5 а)

3. Второй закон Кирхгофа: В замкнутом контуре электрической цепи алгебраическая сумма комплексных амплитуд (действующих значений, ЭДС) равна алгебраической сумме комплексных падений напряжений в нём.

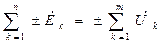. (1.5 б)

Комплексное сопротивление элемента (участка цепи)

Под комплексным сопротивлением понимают отношения комплексной амплитуды входного напряжения к комплексной амплитуде входного тока:

. (1.6)

где Z –модуль комплексного сопротивления, φ=ψ_u - ψ_i – начальная фаза или аргумент комплексного сопротивления; R - активного сопротивления, X– реактивному сопротивлению, причем Z= (R²+X²) ^1/2, а φ_z (ω) =ψ_u-ψ_i =arctg (X/R).

По виду записи комплексного сопротивления можно судить о характере участка цепи: Z =R – активное (резистивное) сопротивление; Z =R+jX — активно-индуктивное сопротивление; Z =R – j X — активно-емкостное

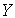- комплексная проводимость, величина, обратная комплексному сопротивлению:

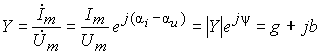
Метод комплексных амплитуд состоит в следующем:

1) исходная схема электрической цепи заменяется комплексной схемой замещения, в которой:

а) все пассивные элементы заменяются их комплексными сопротивлениями, как показано на рис. 4.27.

б) все токи и напряжения в схеме заменяются их комплексными амплитудами, т.е. х (t) = X_m cos(w₀ t – j _x) ® X_m = X_m e^{–j j x}.

Z _L=j w L

L

Z _C= 1/(j w C)

C

Z _R=R

R

Рис. 4.27

2) Расчет электрической цепи сводится к составлению уравнений состояния цепи на основе законов Ома и Кирхгофа в комплексной форме и нахождению комплексных амплитуд токов или напряжений на интересующих нас участках цепи, т.е. Y_m = Y_m e^{–j j y}.

3) Запись окончательного решения состоит в замене рассчитанных комплексных амплитуд на гармонические функции времени, т.е.

Y_m = Y_m e ^{–j j y} ® y (t) = Y_m cos(w₀ t – j _y).

Пример 1. Алгоритм метода рассмотрим на примере анализа цепи, схема которой приведена на рис. 4.29.

Рис. 4.29. RLC -цепь второго порядка

На вход цепи подается синусоидальное воздействие . Параметры воздействия и элементов цепи известны: U_m =1 В, ω =1 с^-1, φ _u =90⁰, R =1 Ом, L =1 Гн, C =1 Ф. Требуется определить токи и напряжения ветвей, построить векторную диаграмму.

Решение.

1. Представим воздействие в комплексной форме:

.

2. Построим схему замещения цепи в частотной области, заменив элементы цепи комплексными двухполюсниками, как это показано на рис. 4.30.

Рис. 4.30. Схема замещения цепи в частотной области

3. Произведем расчет реакций (токов и напряжений) в комплексной области. При этом можно воспользоваться законами Кирхгофа и Ома в комплексной форме, а также известными методами расчета резистивных цепей:

, , ,

,

, ,

,

, .

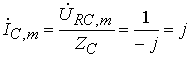3. Построим векторную диаграмму для токов и напряжений в цепи. Для этого на комплексной плоскости откладываются в соответствующем масштабе найденные токи и напряжения, как показано на рис. 4.31.

Рис. 4.31. Векторная диаграмма

Построение векторной диаграммы, как правило, является конечным результатом решения подобных задач. Векторная диаграмма показывает амплитуду и начальную фазу любого тока или напряжения. При необходимости записать временную функцию тока или напряжения, это всегда можно сделать, имея векторную диаграмму. Например, напряжение на L -элементе имеет амплитуду , а начальную фазу 135⁰, значит, во временной области это напряжение можно записать так:

.

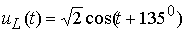Пример 2. Задана эквивалентная схема цепи синусоидального тока (рис. 10) и ее параметры.

Рис. 10.

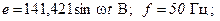
Выполнить следующие действия:

1. Рассчитать токи в ветвях и напряжения на элементах схемы;

2. Составить и проверить баланс полных, активных и реактивных мощностей;

3. Построить векторную диаграмму токов для узла а.

Расчет проводим символическим методом в следующем порядке:

1. Рассчитываем сопротивление всех элементов схемы (учитываем, что )

2. Представляем ЭДС источника в виде комплекса действующего значения. Определяем комплексные сопротивления и проводимости ветвей

.

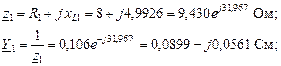
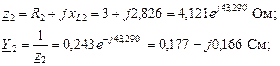
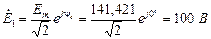3. Рассчитываем токи в ветвях методом двух узлов. Задаем произвольно положительное направление токов в ветвях и положительное направление узлового напряжения. Используя основную формулу метода, рассчитываем узловое напряжение

.

Определяем токи в ветвях, используя обобщенный закон Ома

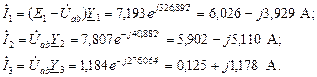
Проверяем корректность промежуточных расчетов, составив уравнение по первому закону Кирхгофа для узла а

.

Комплексная абсолютная погрешность расчета составляет

.

Определяем ее модуль

.

Рассчитываем относительную погрешность определения токов

.

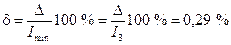Поскольку , расчет токов корректен. Первый пункт задания выполнен.

4. Составляем и проверяем баланс мощностей

Рассчитываем полную комплексную мощность, развиваемую источником, а также его активную и реактивную мощность. При этом используем закон Джоуля – Ленца в комплексной форме записи

,

.

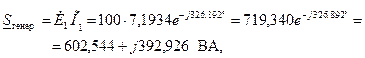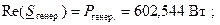
Определяем суммарную активную и реактивную мощность на приемниках. При этом также используем закон Джоуля – Ленца

;

.

Рассчитываем суммарную полную комплексную мощность на приемниках

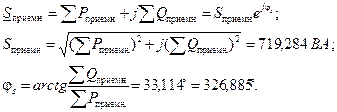
Проверяем корректность расчета, рассчитав модуль относительной погрешности определения полных мощностей

.

Расчет проведен корректно. Второй пункт задания выполнен.

5. Строим векторную диаграмму токов на комплексной плоскости, используя их действительные (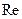) и мнимые () составляющие. Задаемся масштабом по току , делим указанные составляющие токов на масштаб и откладываем получающиеся отрезки в сантиметрах вдоль осей комплексной плоскости (с учетом знаков составляющих).

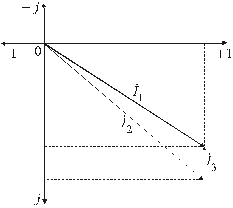
Рис. 11.

Результаты построения (рис. 11) наглядно иллюстрируют корректность проведенных расчетов. Итак, третий пункт и все задание выполнены.

При выполнении задания №2 можно также воспользоваться рекомендуемой литературой [2, 3, 4].

Пример 3 Активное сопротивление катушки R_к=6 Ом, индуктивное X_l=10 Ом. Последовательно с катушкой включено ативное сопротивление R=2Ом и конденсатор сопротивлением х_с=4 Ом (рис.2,а). К цепи приложено напряжение U=50В (действующее значение).

Определить:

1) полное сопротивление цепи;

2)ток;

3)коэффициент мощности;

4)активную, реактивную и полную мощности;

5) напряжения на каждом сопротивлении. Начертите в масштабе векторную диаграмму цепи.

Решение:

1.Определяем полное сопротивление цепи

2.Определяем ток

3.Определяем коэффициент мощности цепи

по таблицам Брадиса находим j=36⁰50’. Угол сдвига фаз j находим по синусу во избежание потери знака угла (косинус является четной функцией)

4.Определяем активную мощность цепи

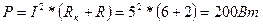
или

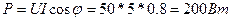
Здесь

5.Определяем реактивную мощность цепи

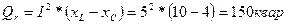
6.Определяем активную мощность цепи

или

7.Определяем падение напряжения на сопротивлениях цепи

; ; ;

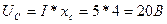
Построение векторной диаграммы начинаем с выбора масштаба для тока и напряжения. Задаемся масштабом по току: в 1см – 1,0А и масштабом по напряжению: 1см- 10В. Построение векторной диаграмм (рис.2,.б) начинаем с вектора тока, который откладываем по горизонтали в масштабе

Вдоль вектора тока откладываем векторы падения напряжения на активных сопротивления U_Rк и U_R:

Из конца вектора U_R откладываем в сторону опережения вектора тока на 90⁰ вектор падения напряжения U_L на индуктивном сопротивлении длиной .Из конца вектора U_I откладываем в сторону отставания от вектора тока на 90⁰ вектор падения напряжения на конденсаторе U_C длиной . Геометрическая сумма векторов U_Rк, U_R, U_L и U_C равна полному напряжению U, приложенному к цепи.

Пример 4:

К электрической цепи, рис. 3.12, а, подведено синусоидальное напряжение частотой f = 50 Гц с действующим значением U = 100 В. Параметры элементов схемы: R ₁ = 30 Ом, L = 0,1 Гн, C = 50 мкФ, R ₂ = 20 Ом. Определить токи в ветвях схемы и показания приборов. Составить баланс мощности. Построить в масштабе векторную диаграмму токов и напряжения.

Рис. 3.12 – Параллельная цепь:
а) схема замещения; б) векторная диаграмма

Дата добавления: 2017-02-01