Решение. Определим комплексные сопротивления каждой ветви.

Решение

Определяем комплексные сопротивления параллельных ветвей. Сопротивление первой ветви

Z ₁ = R ₁ + jX _L,

где

X _L = jωL = 2 πfL = 6,28∙50∙0,1 = 31,4 Ом;

Z ₁ = 30 + j 31,4 Ом.

Комплексное сопротивление второй ветви

Z ₂ = R ₂ – jX _С;

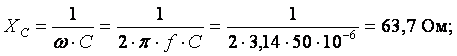
Z ₂ = 20 – j 63,7 Ом.

Находим комплексные значения токов в ветвях

I = I ₁ + I ₂ = 1,6 – j 1,64 + 0,45 + j 1,43 = 2,05 – j 0,21 A.

Действующие значения

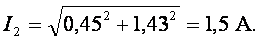
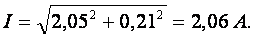
Для определения показания вольтметра составляем уравнение согласно второго закона Кирхгофа для контура б, в, г, д, б. Произвольно выбираем направление обходе контура, показанное на рис. 3.12, а стрелкой

0 = U _бв + R ₂ I ₂ – R ₁ I ₁;

1.. U _бв = R ₂ I ₂ – R ₁ I ₁ = 20·(0,45 + j 1,43) – 30(1,6 – j 1,64) =

= 9 + j 28,6 – 48 + j 49,2 = - 39 + j 77,8;

U _бв = 39 – j 77,8 В.

Вольтметр покажет действующее значение напряжения U _бв

Ваттметр измеряет мощность, потребляемую активной нагрузкой (R ₁ и R ₂).

Известно, что

Р = U · I ·cos φ.

В этом выражении неизвестным является cos φ, где φ угол сдвига между напряжением U и током I. Определить угол φ (или cos φ) можно разными путями. Например, cos φ можно найти из выражения для общего тока, учитывая, что начальная фаза напряжения равна нулю. Для этого обратимся к комплексному значению общего тока

I = 2,05 – j 0,21 A,

где I _R = 2,05 – активная составляющая тока (проекция комплексного вектора полного тока на ось действительных чисел);

I _X = - j 0,21 – реактивная составляющая тока (проекция комплексного вектора полного тока на ось мнимых чисел).

Тогда

где I = 2,06 А – действующее значение общего тока.

Показание ваттметра

Р = 100∙2,06∙0,995 = 205 Вт.

Составим баланс мощностей.

Полная мощность, поступающая от источника

где P _И = 205 Вт; Q _И = 21 Вар.

Мощности приёмников

S_П = Р_П + jQ_П = 205 + j 21,34 ВА.

Результаты расчётов показывают, что баланс мощности сходится, т. е. токи найдены правильно.

Векторную диаграмму строим на комплексной плоскости, рис. 3.12, б. Выбираем масштабы тока и напряжения: 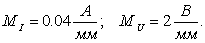(Масштаб выбирается с таким расчётом, чтобы векторная диаграмма занимала примерно половину страницы). Откладываем вектор напряжения совпадающий с осью + 1. Затем откладываем вычисленные значения токов I ₁, I ₂, I. Действительные значения – на оси + 1, мнимые значения – на оси + j.

Пример 6. Для цепи, изображенной на рис. 1 требуется:

1. Определить комплексным методом действующие значения напряжений и токов на всех участках цепи.

2. Определить активные, реактивные и полные мощности каждого участка цепи и всей цепи.

3. Составить баланс активных и реактивных мощностей и оценить погрешность расчета.

4. Построить векторную диаграмму токов и напряжений.

Частота питающего напряжения 50 Гц.

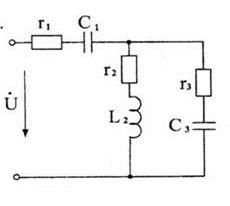
Рис. 1

Исходные данные:
U = 127 В, r1 = 15 Ом, C1 = 60 мкФ, r2 = 10 Ом, L2 = 80 мГн, r3 = 15 Ом, C3 = 90 мкФ.

(Ом)
(Ом)
(Ом)

2. Определим полное сопротивление цепи.

(Ом)

3. Приняв найдем токи и напряжения в ветвях.

(А)

(В)

(В)

(А)
(А)

4. Определим активные, реактивные и полные мощности участков цепи и всей цепи целиком.

Мощность первого участка:
(ВА)
Мощность второго участка:
(ВА)
Мощность третьего участка:
(ВА)
Полная мощность всей цепи:
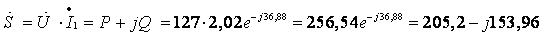(ВА)

Проверим баланс активных мощностей:
P = P1 + P2 + P3
P = 205,2 (BA)
P1 + P2 + P3 = 61,25 + 82,44 + 61,22 = 204,91 (Вт)
Абс. погр-ть Δ = P – (P1 + P2 + P3) = 205,2 – 204,91 = 0,29 (Bт)
Относительная погрешностьть

Проверим баланс реактивных мощноcтей:
S = S1 + S2 + S3
S =- 153,96 (BA)
S1 + S2 + S3 = - 216,7 + 207,19 – 144,5 = - 154,01 (ВА)
Абс. погр-ть Δ = |S – (S1 + S2 + S3)| = |153,96 – 154,01| = 0,05 (BA)
Отн. погр-ть

5. Построим векторную диаграмму на комплексной плоскости.

Для этого определим напряжения на каждом элементе схемы.
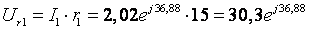(В)
(В)
(В)
(В)
(В)
(В)

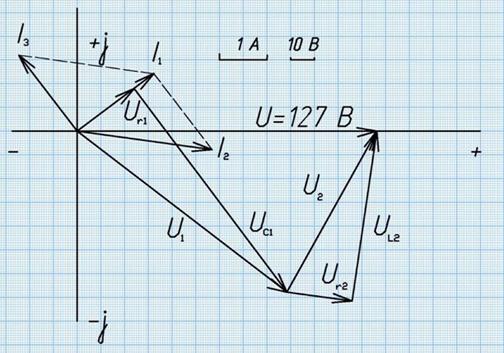
Рис. 2. Векторная диаграмма.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЗАДАНИЙ по теме "ТРЕХФАЗНОЙ ЦЕПИ"

II. Краткие теоретические положения.

3.1. Трёхфазная система питания потребителей электроэнергии.

Трёхфазная система питания электрических цепей представляет собой совокупность трёх синусоидальных ЭДС или напряжений, одинаковых по частоте и амплитудному значению, сдвинутых по фазе относительно друг друга на угол 120.

E_A = E_Am sin wt

E_B = E_Bm sin (wt-2 /3)

E_C = E_Cm sin (wt+2 /3).

В симметричных источниках питания максимальные значения ЭДС равны, соответственно равны и действующие значения ЭДС

E_A=E_B=E_C= Eф. Пренебрегая внутренним сопротивлением источника, можно принять соответствующие ЭДС источника равными напряжениям, действующим на его зажимах:

E_A=U_A, E_B=U_B, E_C=U_C.

Комплексные напряжения симметричного источника питания могут быть представлены системой уравнений:

.

Ua = Uф e ^j0 = Uф,

.

Ub = Uф e^-j120 = Uф(-0,5- j 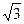/2),

.

Uс = Uф e^+j120 = Uф(-0,5+ j 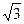/2)

Фазным называется напряжение между началом и концом фазы. Линейным назовём напряжение между двумя линиями или между началами двух фаз. Соотношение между линейным и фазным напряжениями симметричного источника питания: U_Л = 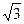Uф.

3.2. Трёхфазные электрические цепи при соединении фаз приёмников “звездой”.

При соединении фаз трёхфазного источника питания “звездой” концы фаз источника X,Y,Z объединены в общую нейтральную точку N, а начала фаз А,В,С подключаются к соответствующим линейным проводам Аа, Вв, Сс. Аналогичным образом при соединении трёхфазных потребителей объединяются в нейтральную точку n концы его фаз x,y,z, при начала фаз а,в,с подключаются к линейным проводам.

Линейные токи In в питающих линиях имеют условно-положительное направление от источника энергии к приёмнику. При соединении приёмника энергии по схеме “звезда” линейные токи I_A,I_B,I_C одновременно являются и фазными токами приёмника Iа,Iв,Iс, т.е.

I_A= Iа; I_B = Iв; I_C = Iс.

Трёхфазные источники питания практически всегда выполняются симметричными. Трёхфазные потребители электроэнергии могут быть симметричными и несимметричными. Для симметричных приёмников электроэнергии справедливы соотношения, полученные для трёхфазных симметричных источников питания.

При этом Ua = Ub=Uc=Uф; U_AB = U_BC =U_CA = U_Л; Za=Zb=Zc=Zф;

cosΨa = cosΨb = cosΨc = CosΨф; U_Л= 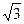Uф.

Для несимметричных приёмников не все эти соотношения соблюдаются.

При анализе трёхфазных электрических цепей широко используется метод комплексных чисел.

При несимметричной нагрузке комплексные сопротивления фаз приёмника не одинаковы (Za≠Zb≠Zc), при этом комплексное напряжение UnN, действующее между нейтральными точками N и n системы, определяют по методу двух узлов

....

U_nN =

Дата добавления: 2017-02-01