Выбор вида модели и оценка ее параметров

Как и в парной зависимости возможны различные виды множественной регрессии: линейные и нелинейные. В виду четкой интерпретации параметров наиболее широко используются линейная и степенные функции.

В уравнении множественной регрессии:

(41)

Коэффициенты при переменных х называются коэффициентами «чистой» регрессии. Они показывают среднее изменение результата с изменением соответствующего фактора на единицу при неизменном значении других факторов, закрепленных на среднем уровне.

Параметр а не подлежит экономической интерпретации.

Анализ уравнения регрессии и методика определения его параметров становятся более наглядными, а расчеты существенно упрощаются, если воспользоваться матричной формой записи этого уравнения. Так, уравнения вида

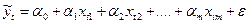(42)

можно записать следующим образом:

,

где Y – вектор зависимой переменной размерности (n х 1), представляющий собой n наблюдений значений y_t.

X – матрица независимых переменных, элементы которой суть n x m наблюдения значений независимых переменных X_1, X_{2, …,} X_m размерность данной матрицы равна (n x m);

α – подлежащий оцениванию вектор неизвестных параметров размерности (m х 1 );

ε – вектор случайных отклонений (возмущений) размерности (n х 1).

Таким образом,

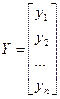
Х =

1 x11.... x1m 1 x21.... x2m ................ 1 xn1.... xnm

Уравнение (42) содержит значения неизвестных параметров α₀, α_1, α_{2, …,} α_m. эти величины оцениваются на основе выборочных наблюдений, поэтому полученные расчетные показатели не являются истинными, а представляют собой лишь их статистические оценки. Модель линейной регрессии, в которой вместо истинных значений параметров представлены их оценки (а именно такие регрессии и применяются на практике), имеют вид:

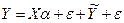(43)

где α – вектор оценок параметров;

ε – вектор «оцененных» отклонений регрессии, ε = Y – Xα – остатки регрессии;

– оценка значений Y, равная Xα.

Для оценивания неизвестного вектора параметров α воспользуемся методом наименьших квадратов (МНК). Формула для вычисления параметров регрессионного уравнения имеет вид:

α = (Х^ТХ)^-1Х^ТУ (44)

Можно воспользоваться и другим способом оценки неизвестных параметров регрессионного уравнения.

Для линейных моделей и нелинейных уравнений, приводимых к линейным, строится следующая система нормальных уравнений, решение которых позволяет получить оценки параметров регрессии:

(45)

для ее решения может быть применен метод определителей:

(46)

где 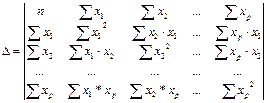- определитель системы.

- частные определители; которые получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы.

Для оценки параметров нелинейных уравнений используют 2 подхода:

1. основан на линеаризации модели и заключается в том, что с помощью подходящих преобразований исходных переменный исследуемую зависимость представляют в виде линейного соотношения между преобразованными переменными.

2. обычно применяют в случае, когда подобрать соответствующее линеаризационное преобразование невозможно. В этом случае применяют методы нелинейной оптимизации на основе исходных переменных.

Коэффициенты условно чистой регрессии, т.е. b_j являются именованными числами, выраженными в различных единицах измерения, в тех же единицах, что и соответствующие им факторы. Поэтому они не сравнимы друг с другом, т.е. по их величине нельзя сделать вывод, какой из факторов в наибольшей степени влияет на результат. Для приведения их в сравнимый вид применяется то же преобразование, что и для получения парных коэффициентов. Полученную величину называют стандартизированным коэффициентом регрессии.

Стандартизированный коэффициент регрессии рассчитывается по формуле

(47)

β_j – коэффициент при факторе х_j. определяет силу влияние вариации х_j на вариацию результативного признака у при отвлечении от сопутствующего влияния вариаций других факторов, входящих в уравнение регрессии.

Т.к. β_j сравнимы между собой, то по величине данных коэффициентов можно ранжировать факторы по силе их воздействия на результат.

Смысл стандартизированных коэффициентов β_j позволяет использовать их при отсеве факторов, т.е. из модели исключаются факторы с наименьшим значением β_j.

Коэффициенты условно чистой регрессии можно выразить в виде относительно сравнимых показателей связи – средних коэффициентов эластичности.

(48)

Средний коэффициент эластичности показывает, что при изменении фактора х_j на 1% результативный признак изменяется на Э_j % его средней величины при неизмененном влиянии всех остальных факторов.

Дата добавления: 2017-02-01