Оценка параметров модели

3. С помощью аналитического метода

3а) Проведем оценку параметров модели:

На основе метода наименьших квадратов (МНК) проведем оценку параметров регрессии по формуле:

При этом используем данные, приведенные в таблице 2.2

Таблица 2.2. – Исходная информация

Y	Хо	X2	X5
Объем реал.		Реклама	Инд. п. расх.
		5,2
		4,5
		6,7
		6,8
		7,8
		3,9
		5,1
		3,9
		3,8
		3,8
		5,5
		6,7
		8,9
		9,1
		10,3
		12,7
		13,8
		14,9

Для вычисления вектора оценок параметров регрессии воспользуемся следующими встроенными в Exel функциями:

МУМНОЖ – умножение матриц,

ТРАНСП – транспонирование матриц,

МОБР – вычисление обратной матрицы.

Для вычисления вектора оценок параметров регрессии a в Exel необходимо выполнить следующие действия:

1) ввести данные (таб. 2.2);

2) выделить диапазон ячеек для записи вектора α, соответствующий его размерности (3х1);

3) используя встроенные в Exel функции, ввести формулу

α = (Х^ТХ)^-1Х^ТУ,

определяющую вектор α.

4) нажать одновременно клавиши CTRL+SHIFT+ENTER. Появится результат (рис. 2.6).

Рис. 2.6. Результаты вычислений – вектор оценок параметров
регрессии a.

Таким образом, имеем

a₀ 166,9265419

a = a₁ = 1,671226055

a₂ 0,723160336

Уравнение регрессии зависимости объема реализации от затрат на рекламу и индекса потребительских расходов можно записать в виде:

Расчетные значения Y определяются путем последовательной подстановки в эту модель значений факторов, взятых для каждого момента времени t (табл.2.3).

Таблица 2.3. – Расчетные значения

Набл.	Y	Предск. Y	e(t)	e^2(t)	(e(t)- e(t-1))^2	Аi,%	e(t)e(t-1)	(Y-Yср)^2
		224,0687	-2,0687	4,279354	-	0,931829
		225,7914	-2,7914	7,792154	0,522415	1,251768	5,774546
		230,9145	-0,9145	0,836239	3,523061	0,397592	2,552666
		225,2963	6,7037	44,93958	58,03636	2,889525	-6,13027
		237,0918	-5,0918	25,92614	139,1331	2,194729	-34,1337
		232,0203	7,9797	63,67544	170,8631	3,324871	-40,6308
		240,5342	-0,5342	0,285396	72,48674	0,222594	-4,26295
		239,9751	-27,9751	782,6048	753,0002	13,19579	14,94498
		264,3954	-14,3954	207,2276	184,4075	5,758161	402,7125
		247,0396	3,9604	15,68512	336,9372	1,577866	-57,0122
		243,2597	10,7403	115,3531	45,96584	4,228447	42,53619
		245,5417	8,4583	71,54322	5,207221	3,330048	90,84455
		243,9313	15,0687	227,0643	43,69647	5,818013	127,4555
		254,8396	9,1604	83,91205	34,90802	3,46983	138,0342
		256,6202	7,3798	54,46125	3,170415	2,795374	67,60144
		259,3488	6,6512	44,23786	0,530904	2,500434	49,0841
		251,7892	-31,7892	1010,555	1477,663	14,44965	-211,435
		263,0287	4,9713	24,71427	1351,339	1,854979	-158,035
		267,7596	1,2404	1,53848	13,92029	0,461098	6,16623
		266,7538	3,2462	10,53783	4,023428	1,202297	4,026443
Σ			0,0000	2797,169	4699,334	71,85489	440,0932

Проведем проверку качества модели. Для начала определим автокорреляцию остатков. Для этого используем d-критерий Дарбина – Уотсона. Для определения величины d-критерия воспользуемся расчетной таблицей 2.3.

Выдвинем гипотезу Н_о об отсутствии автокорреляции остатков.

d= =

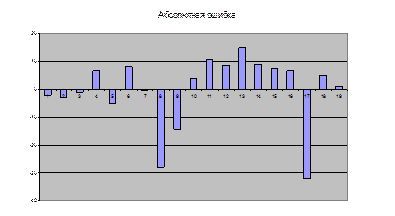
Рис. 2.7. График остатков

В качестве критических табличных уровней при n = 20, k=2, при уровне значимости g = 0,05 согласно приложению 3: d_L = 1,10 и d_u = 1,54.

Расчетное значение d = 1,68 попало в интервал от d_u=1,54 до 4- d_u =2,46, следовательно нулевая гипотеза подтверждается. Автокорреляция остатков отсутствует. Необходимости проводить дальнейшую проверку с помощью коэффициента автокорреляции первого порядка нет.

3б) Оценим модель через среднюю ошибку аппроксимации.

Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических. Допустимый предел значений - не более 8 – 10%.

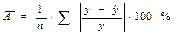= = 71,85489/20=3,59

В среднем расчетные значения отклоняются от фактических на 3,59%. Это значение входит в допустимый предел, следовательно, качество построенной модели достаточно высокое.

3в) Вычислим для построенной модели множественный коэффициент детерминации

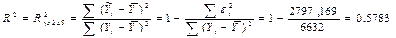
Множественный коэффициент детерминации показывает долю вариации результативного признака под воздействием включенных в модель факторов Х₂ и Х₅. Т.о., почти 58% вариации зависимой переменной (объема реализации) в построенной модели обусловлено влиянием включенных факторов Х₂ (расходы на рекламу) и Х₅ (индекс потребительских расходов).

Проверку значимости уравнения регрессии проведем на основе F-критерия Фишера.

Выдвигаем нулевую гипотезу Но о статистической незначимости полученного уравнения регрессии.

В нашем примере k₁=2; k=20-2-1=17.

Таким образом. F _{табл .}=3,59 при =0,05 (приложение 1).

Т.к. F _{факт .}> F _табл., то при заданном уровне вероятности g=0,05 следует отвергнуть нулевую гипотезу о статистической незначимости уравнения регрессии и показателя тесноты связи. Необходимо признать уравнение регрессии адекватным.

Значимость коэффициентов уравнения регрессии a₁ и a₂ оценим с использованием t-критерия Стьюдента:

=

=

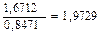
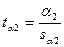Табличное значение t-критерия Стьюдента при уровне значимости 0,05 и степенях свободы (20-2-1)=17 составляет t_табл=2,11 (приложение 2).

Так как t_a1=1,97 < t_табл=2,11, следует принять нулевую гипотезу о незначимости коэффициента a₁.

t_a2=3,66 > t_табл=2,11, гипотеза о незначимости коэффициента a₂.

4. С цельюпроверки полученныхрезультатов проведем регрессионный анализ выбранной модели с помощью Exel, применив инструмент Регрессия.

Для проведения регрессионного анализа с помощью Exel выполните следующие действия:

1) выберите команду Сервис/Анализ данных;

2) в диалоговом окне Анализ данных выберите инструмент Регрессия. Щелкните по кнопке ОК.

3) в диалоговом окне Регрессия в поле «Входной интервал У» введите адрес диапазона ячеек, который содержит зависимую переменную. В поле «Входной интервал Х» введите адреса одного или нескольких диапазонов, которые содержат значения независимых переменных. Если выделены заголовки столбцов, то установите флажок «Метки в первой строке»;

4) выберите параметры вывода. В поле «Остатки» поставьте необходимые флажки. Щелкните по кнопке ОК.

Сравнивая полученные в п.п. 1,3 результаты с результатами, полученными с помощью Exel (рис. 2.8), убеждаемся в правильности выполненных действий.

5. Проанализируем влияние факторов на зависимую переменную

Учитывая, что коэффициенты регрессии невозможно использовать для непосредственной оценки влияния факторов на зависимую переменную из-за различия единиц измерения, вычислим соответствующие коэффициенты эластичности, b-коэффициенты:

,

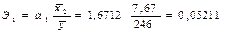Таким образом, при увеличении расходов на рекламу на 1% от своего среднего значения величина объема реализации увеличится на 0,05%, при увеличении потребительских расходов на 1% величина объема реализации увеличится на 0,27%.

Рис. 2.8. Результаты регрессионного анализа, проведенного с помощью Exel. [2]

Кроме того, по величине b-коэффициентов, можем сделать вывод, что наибольшее влияние на изменение объема реализации оказывает фактор Х₅ (индекс потребительских расходов), наименьшее Х₂ (расходы на рекламу). При увеличении индекса потребительских расходов на 15,5505 ед. объем реализации увеличится на 11 тыс. руб.(0,6019∙18,6829≈11), а при увеличении расходов на рекламу на 3,8043 ед. объем реализации увеличится на 5 тыс. руб. (0,2759∙18,6829≈5).

6. С помощью Exel выберем наилучший вид тренда временных рядов, соответствующих оставленным в модели переменным.

На рис. 2.9 приведен результат построения трендов для временного ряда «Затраты на рекламу». В качестве аппроксимирующей функции выбран полином второй степени – парабола (т.к. по данной модели наибольшее значение у коэффициента множественной детерминации), по которой построен прогноз на два шага вперед. Значение коэффициента детерминации составило R²=0,853, что указывает на то, что весьма большая доля вариации признака Y учтена в модели (более, чем 85% вариации результативного признака объясняется вариацией фактора «затраты на рекламу».

Рис. 2.9. Результат построения тренда и прогнозирования по тренду для временного ряда «Затраты на рекламу»

Аппроксимирующая функция: Х₂=7,2449-0,7933t+0,0603t².

Прогнозные значения на два шага вперед соответственно составляют:

Х₂(21)=7,2449-0,7933∙21+0,0603∙21²=17,1779,

Х₂(22)=7,2449-0,7933∙22+0,0603∙22²=18,9775.

Для фактора Х₅ «Индекс потребительских расходов» выбираем полиноминальную модель пятой степени (этой модели соответствует наибольшее значение коэффициента детерминации):

Х₅ = – 0,0005271347t₅ + 0,0333138764t₄ – 0,7481642428t₃ + 6,9818484692 t₂ – 21,4309347217t + 86,0069143467

Прогнозные значения на 21 и 22 периоды соответственно составляют:

Х₅(21) = 112,248,

Х₅(22) = 114,6053.

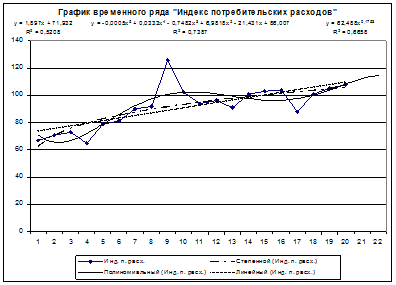
Рис. 2.10. Результат построения тренда и прогнозирования по тренду для временного ряда «Индекс потребительских расходов».

7. Для получения прогнозных оценок переменной Y по модели

Подставим в нее найденные прогнозные значения факторов Х₂ и Х₅, получим:

(21)= 166,9265+1,6712∙17,1779+0,7232∙112,248=276,81195,

(22)= 166,9265+1,6712∙18,9778+0,7232∙114,6053=281,52475.

Доверительный интервал прогноза имеет границы:

верхняя граница прогноза: ,

нижняя граница прогноза: ,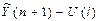

где U(l)= ,

Имеем

t_кр =2,11 (по таблице при g=0,05 и числе степеней свободы 17),

1

Х _пр (21) = 17,1779

112,248

1

Х _пр (22) = 18,9775

114,6053

Тогда с использованием Exel, имеем

= 0,411376247,

U(l)=12,8273∙2,11∙ =17,3595

= 0,469169297

U(l)=12,8273∙2,11∙ =18,5388

Результаты прогнозных оценок модели регрессии представим в таблице прогнозов (табл. 2.4).

Таблица 2.4. – Результаты прогнозных оценок модели регрессии

Упреждение	Прогноз	Нижняя граница	Верхняя граница
	276,81195	259,45245	294,17145
	281,52475	262,98595	300,06355

Дата добавления: 2017-02-01