Вынужденные механические колебания. Резонанс

Вынужденные механические колебания происходят, когда на систему, кроме упругой силы и силы сопротивления, действует сила, величина которой меняется с течением времени по гармоническому закону. Эта внешняя сила периодически пополняет энергию системы, расходуемую на работу против силы сопротивления. Поэтому в системе с течением времени устанавливаются вынужденные колебания с постоянной амплитудой.

Запишем II закон Ньютона для этого случая:

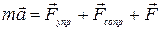, (5.71)

где 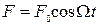, - частота внешней силы. (5.72)

В проекции на направление движения (ось 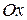) это уравнение имеет вид:

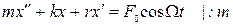
Введем обозначения: ; ; .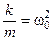

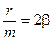(5.73)

- это дифференциальное уравнение вынужденных механических колебаний. Общее решение этого неоднородного дифференциального уравнения представляет собой сумму общего решения соответствующего однородного дифференциального уравнения и частного решения неднородного уравнения:

. (5.74)

С течением времени первое слагаемое в этом выражении быстро уменьшается, поэтому установившиеся вынужденные колебания описываются вторым слагаемым. График зависимости x(t) в этом случае изображен на рис. 5.18.

Частота установившихся вынужденных колебаний равна частоте внешней силы , амплитуда 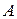и начальная фаза 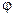определяются соотношениями:

, (5.75)

. (5.76)

Начальная фаза 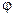в данном случае определяет сдвиг по фазе между установившимися вынужденными колебаниями и внешней силой.

Проанализируем зависимость амплитуды установившихся колебаний 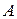от частоты внешней силы :

1) , ;

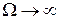2) , 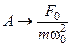; (5.77)

3) в системе, совершающей вынужденные колебания, возможно явление резонанса.

Резонанс – это резкое возрастание амплитуды вынужденных колебаний при определенной частоте внешней силы. Найдем резонансную частоту. Для этого производную по от 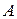приравняем к нулю:

; ,

; .

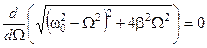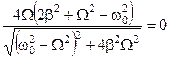Два корня этого уравнения (при и 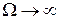) соответствуют минимумам 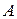. При

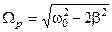(5.78)

амплитуда установившихся вынужденных колебаний достигает максимального значения. Это и есть резонансная частота.

Рис.5.19

Найдем амплитуду колебаний при резонансе:

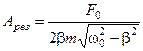. (5.79)

Зависимости 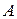от называются резонансными кривыми. Резонансные кривые в случае острого резонанса (затухание мало, ) и тупого резонанса (сильное затухание, ) представлены на рис. 5.19. Острота резонанса, т.е. высота и ширина резонансного пика, зависят от коэффициента затухания .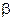

Дата добавления: 2014-01-04