Вынужденные электромагнитные колебания

Вынужденные электромагнитные колебания возникают в колебательном контуре, в котором действует ЭДС, величина которой меняется по гармоническому закону.

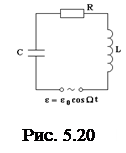Запишем закон сохранения энергии для колебательного контура, изображенного на рис. 5.20:

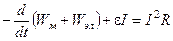, (5.80)

.

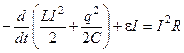Введем обозначения:

; ; ; ;

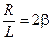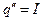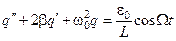(5.81)

- дифференциальное уравнение вынужденных электромагнитных колебаний. Оно аналогично (5.73). Решение этого уравнения имеет вид, аналогичный (5.74):

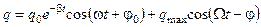. (5.82)

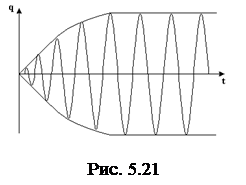
График этой зависимости представлен на рис. 5.21.

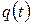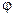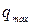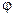Установившиеся вынужденные колебания описываются вторым слагаемым в зависимости . Они происходят с частотой ЭДС , - разность фаз между колебаниями заряда и внешней ЭДС. и определяются соотношениями, аналогичными (5.75) и (5.76):

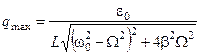, (5.83)

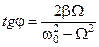. (5.84)

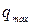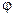Видно, что и определяются свойствами контура и вынуждающей ЭДС, причем 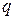отстает по фазе от .

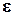В электрической цепи, обладающе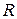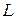й , и , в которую включена переменная ЭДС, возможны явления резонанса заряда и резонанса тока.

1). Резонанс заряда (напряжения).

Для нахождения резонансной частоты, аналогично тому, как это сделано в разделе 5.8, нужно взять производную по частоте ЭДС от 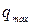и приравнять её нулю.

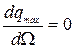. Проделав соответствующие преобразования, получим:

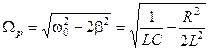(5.85)

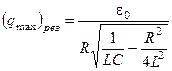. (5.86)

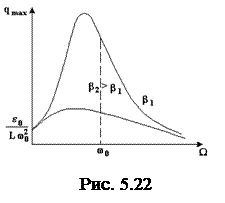
Резонансные кривые для резонанса заряда представлены на рис. 5.22.

2. Для нахождения резонансной частоты при резонансе тока найдем ток в контуре, используя соотношение :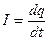

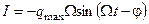. (5.87)

Амплитуда тока равна

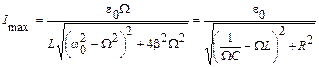. (5.88)

Как видно из этого выражения, амплитуда тока принимает наибольшее значение при такой частоте внешней ЭДС, при которой 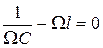. Из этого соотношения находим резонансную частоту для резонанса тока

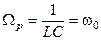(5.89)

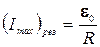. (5.90)

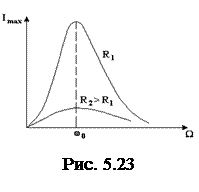
Резонансные кривые для резонанса тока представлены на рис. 5.23. Острота резонанса зависит от активного сопротивления цепи .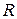

Дата добавления: 2014-01-04