Краткая теория. Определение постоянной Ридберга и массы электрона

Аппаратура

ОПРЕДЕЛЕНИЕ ПОСТОЯННОЙ РИДБЕРГА И МАССЫ ЭЛЕКТРОНА

3.1. Цель и содержание работы: ознокомление со спектром и системой энергетических состояний атома водорода. Изучение сериальной закономерности в спектре водорода, экспериментальное измерение длин волн серии Бальмера, определение спектроскопическим методом постоянной Ридберга и массы электрона; определение энергии ионизации, уровней энергии и размеров атома водорода в различных квантовых состояниях.

Монохроматор УМ-2, ртутная лампа, газоразрядная трубка с водородом, катушка Румкорфа, блок питания.

В результате исследований, проведенных во второй половине XIX в., было установлено, что пары каждого химического элемента при соответствующем возбуждении излучают вполне определенный спектр, состоящий из совокупности отдельных линий - так называемый линейчатый спектр. Причем атомам каждого химического элемента соответствует свой вполне определенный линейчатый спектр.

Таким образом, были заложены основы спектрального анализа - физического метода определения качественного и количественного состава вещества путем изучения его спектров (Кирхгоф, Бунзен, 1859). Анализ линейчатых спектров элементов сразу же привел к заключению, что линии в спектрах расположены не произвольно, беспорядочно, а закономерно. Возникла задача установить и объяснить эти закономерности.

Изучая линейчатый спектр водорода, швейцарский учитель физики И.Бальмер установил (1885), что длины волн известных в то время девяти линий спектра могут быть вычислены по формуле

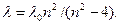(3.1)

Формулу (3.1)обычно записывают в виде

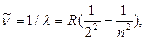(3.2)

где R=10973731,77м^-1, n=3,4,5.... 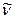=1/λ -называется волновым числом. Константа R впервые была определена Ридбергом Р. и называется постоянной Ридберга. Формула Бальмера, впервые указавшая на особое значение целых чисел в спектральных закономерностях, сыграла выдающуюся роль в развитии учения о строении атомов. Если учесть большую точность спектроскопических измерений, то следует признать, что формула Бальмера принадлежит к числу наиболее точных закономерностей физики. Из формулы (3.2) видно, что все линии, отличающиеся различными значениями n, образуют группу, или серию, линий, называемую серией Бальмера. С увеличением n линии серии сближаются друг с другом. Значение n=определяет границу серии Бальмера. Ей соответствует длина волны λ_гр=3645,068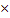10^-10 м.

Ридберг показал, что в линейчатых спектрах не только водорода, но и других элементов наблюдаются спектральные серии, причем волновые числа 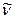всех линий данной серии удовлетворяют соотношению

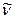=T(n₂)-T(n₁), (3.3)

где n₁ и n₂ -некоторые целые числа. Функции Т(n₂) и Т(n₁) называются спектральными термами. Для данной серии n₂ имеет постоянное значение. Изменение числа n₁ дает все линии данной серии.

Тщательные исследования спектра водорода показали, что в нем наблюдаются пять серий спектральных линий. В ультрафиолетовой области спектра была обнаружена серия Лаймана

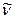=1/λ=R, (3.3)

где n=2,3,4...

В инфракрасной области были обнаружены:

серия Пашена 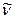=R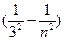, где n=4,5,6...

серия Брэкета 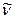=R, где n=5,6,7...

серия Пфунда 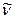=R, где n=6,7,8...

серия Хэмфри 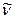=R, где n=7,8,9...

Таким образом, все сериальные формулы спектра водорода могут быть выражены единой формулой

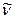=1/λ=R 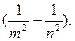(3.4)

Линейчатый спектр атома водорода и закономерности (3.4) находятся в прямом противоречии с классическим истолкованием модели атома Резерфорда.

Применение классической электродинамики к ядерной модели атома привело к полному противоречию с экспериментальными фактами. Согласно классической теории, должны иметь место:

а) непрерывная потеря электроном энергии в виде излучения электромагнитных волн и неустойчивость атома;

б) существование только непрерывного спектра. Спектральных линий существовать не должно.

В действительности оказывается, что а) атом является устойчивой системой; б)атом излучает энергию лишь при определенных условиях; в) излучение атома имеет линейчатый спектр.

Выход из создавшегося противоречивого положения был предложен Бором (1913). В основе теории Бора лежала идея связать в единое целое эмпирические закономерности линейчатых спектров, ядерную модель атома Резерфорда и квантовый характер излучения и поглощения света (гипотеза Планка), подтвержденные обширным экспериментальным материалом. Бор сформулировал законы, описывающие состояние и движение электронов в атоме в виде определенных постулатов. Постулаты эти таковы:

1. Электрон в атоме может вращаться только по строго определенным стационарным орбитам, радиусы которых определяются из условия

, (3.5)

где L – момент импульса электрона; n – главное квантовое число, принимающее положительное значение 1,2... и определяющее принадлежность электрона к той или иной орбите; h -постоянная Планка. Все другие орбиты «запрещены». Таким образом, Бор постулировал, что энергия электрона в атоме может принимать строго определенные дискретные значения Е₁,Е₂,....Е_n... Вращаясь по стационарным орбитам, электрон не излучает и не поглощает электромагнитных волн.

2. Излучение происходит лишь при переходе электрона из стационарного состояния с большим значением энергии Е_k в другое стационарное состояние с меньшим значением энергии Е_i. При этом излучается квант энергии (фотон) строго определенной частоты. Излучение атома монохроматично, и частота его определяется фундаментальным соотношением (условие частот Бора)

E_k–E_i =hν_ik, (3.6)

где hν_ik -энергия излученного фотона.

Из соотношения (3.6) следует, что излучение происходит при переходе электрона с внешних орбит на внутренние. Если же электрон переходит с внутренних орбит на внешние, то энергия поглощается.

Сопоставление формулы (3.6) и (3.4) позволяет заключить, что энергия атома в некотором сстационарном состоянии

E_n=-Rhc/n²=-2πћRc/n² где n=1,2,...., (3.7)

а спектральный терм связан с энергией атома формулой

T(n)=-E_n/hc=R/n² (3.8)

Таким образом, целые числа, входящие в сериальные формулы (3.4) определяют квантовые значения энергии атома (энергетические уровни атома). Из формулы (3.7) следует, что энергетические состояния атома водорода образуют последовательность энергетических уровней, изменяющихся в зависимости от значения n. Энергетическое состояние, соответствующее значению n=1, называется основным или нормальным (невозбужденным) состоянием. Все состояния с n>1 называются возбужденными. При n→, →0. Знак минус в формуле (3.7) показывает, что электрон связан в атоме силой притяжения к ядру. Поэтому абсолютное значение E_n в формуле (3.7) считают энергией связи электрона в атоме, находящегося в состоянии n.

На рис. 3.1. приведена схема энергетических уровней атома водорода. Стрелками указаны переходы, соответствующие излучению различных серий спектральных линий.

Постулаты позволили Бору рассчитать спектр атома водорода и водородоподобных ионов, а также теоретически вычислить соответствующие им значения постоянной Ридберга, находящиеся в хорошем согласии с опытом. Бор считал, что движение электрона в водородоподобной системе происходит по круговой орбите радиуса r под действием кулоновской силы притяжения электрона к ядру, обусловливающей центростремительное ускорение, т.е. можем записать:

(3.9)

Из формулы (3.9), (3.5) получим

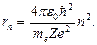(3.10)

Энергия электрона в водородоподобной системе равна сумме кинетической энергии Е_k и потенциальной E_п энергии в электростатическом поде ядра

E=E_k+E_п=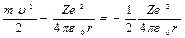 (3.11)

Подставив r в (З.ІІ) из (3.10) получим

(3.12)

Сравнивая формулы (3.7) и (3.12), получим

(3.13)

Теоретическое значение немного отличается от экспериментального значения R. Расхождение объясняется тем, что при выводе формулы (3.13) ядро атома считалось неподвижным (ему приписывалась бесконечно большая масса). В действительности же ядро имеет конечную массу, вследствие чего происходят движения как электрона, так и ядра вокруг центра масс атома, поэтому вместо массы m электрона в в формулу (3.13) следует ввести приведенную массу: µ=mM/(m+M), где M масса ядра. Тогда

(3.14)

Следовательно, постоянная Ридберга должна зависеть от массы ядра:

(3.14а)

Приведенная масса µ будет иметь различные значения для разных изотопов, что приводит к некоторому различию уровней энергии и длин волн спектральных линий. Это явления называется изотопическим сдвигом. Именно по изотопическому сдвигу и был открыт тяжелый изотоп водорода – дейтерий (1932г.). Полученное, таким образом значение R для водорода находится в хорошем согласии с данными, полученными из спектроскопических измерений.

Дата добавления: 2014-01-04