
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Числовые множества
|
|
|
|
I. Символы и обозначения
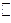 – знак параллельности – знак параллельности
| 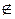 – знак «не принадлежит» – знак «не принадлежит»
|
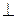 – знак перпендикулярности – знак перпендикулярности
| 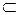 – знак включения – знак включения
|
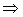 – знак следования – знак следования
| 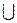 – знак объединения – знак объединения
|
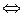 – знак равносильности (эквивалентности) – знак равносильности (эквивалентности)
| 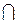 – знак пересечения – знак пересечения
|
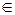 – знак принадлежности – знак принадлежности
| 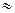 – знак приближённого равенства – знак приближённого равенства
|
II. Множества. Определения этого понятия нет. Под множеством будем понимать совокупность некоторых объектов. При этом множество должно быть описано так, чтобы можно было понять, принадлежит тот или иной объект данному множеству или нет. Описать то или иное множество можно, например, перечислением его элементов или описанием характерных свойств элементов.
Множество, не содержащее ни одного элемента, обозначается символом
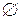 – пустое множество.
– пустое множество.
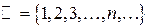 – множество натуральных чисел;
– множество натуральных чисел;
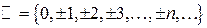 – множество целых чисел;
– множество целых чисел;
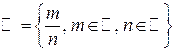 – множество рациональных чисел;
– множество рациональных чисел;
I – множество иррациональных чисел – нерациональные числа, которые можно представить в виде бесконечной непериодической десятичной дроби;
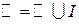 – множество действительных чисел.
– множество действительных чисел.
Числовые промежутки представляют собой подмножества множества :
:
отрезок 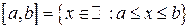 ;
;
интервал 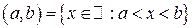 ;
;
полуинтервалы 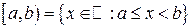 ,
, 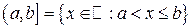 ;
;
бесконечные промежутки 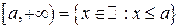 ,
, 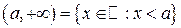 ,
, 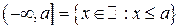 ,
, 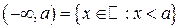 ,
, 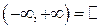 .
.
III. Основные алгебраические соотношения
Действия со степенями и логарифмами
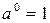
| 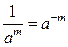
| 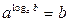
| 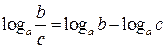
|
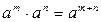
| 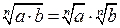
| 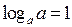
| 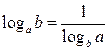
|
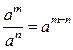
| 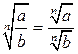
| 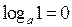
| 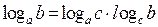
|
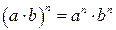
| 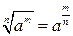
| 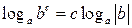
| 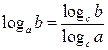
|
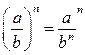
| 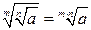
| 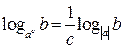
| 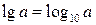
|
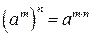
| 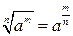
| 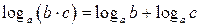
| 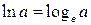
|
Формулы сокращенного умножения
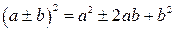
| 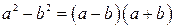
|
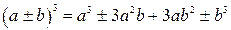
| 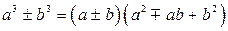
|
Корни квадратного уравнения 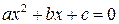
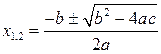
|
Разложение квадратного трехчлена на множители
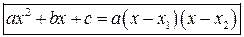 , где
, где 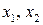 – корни уравнения
– корни уравнения 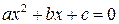 .
.
Выделение полного квадрата в квадратном трехчлене
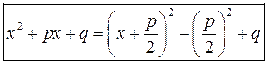 .
.
IV. Основные тригонометрические соотношения рис
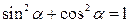
| 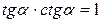
| 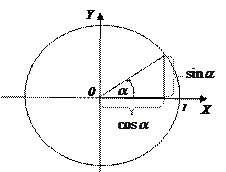
|
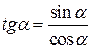
| 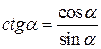
| |
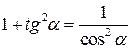
| 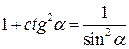
| |
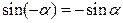
| 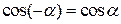
|
Сумма и разность двух аргументов
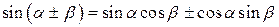
| 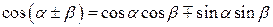
|
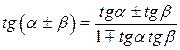
| 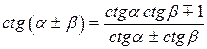
|
Двойные аргументы
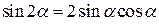
| 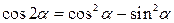
| 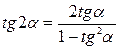
| 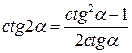
|
Формулы понижения степени
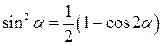
| 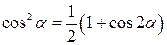
|
Преобразование произведения в сумму
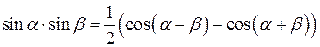
| 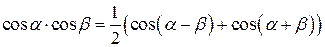
|
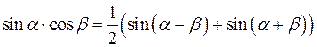
|
Преобразование суммы и разности в произведение
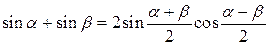
| 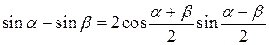
|
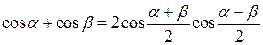
| 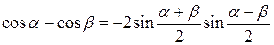
|
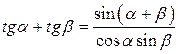
| 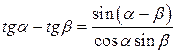
|
Некоторые значения тригонометрических функций
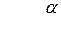
| 
| 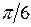
| 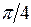
| 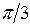
| 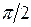
| 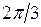
| 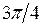
| 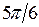
| 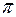
|
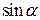
| 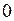
| 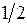
| 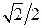
| 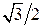
| 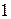
| 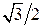
| 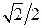
| 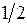
| 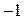
|
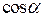
| 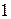
| 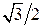
| 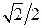
| 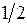
| 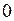
| 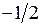
| 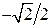
| 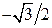
| 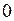
|

| 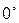
| 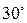
| 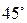
| 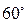
| 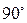
| 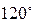
| 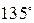
| 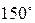
| 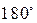
|
Тригонометрические уравнения
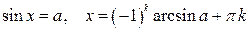
| 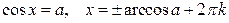
|
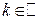
|
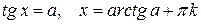
| 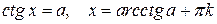
|
Раздел 1. ЛИНЕЙНАЯ АЛГЕБРА
§1. МАТРИЦЫ
|
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 370; Нарушение авторских прав?; Мы поможем в написании вашей работы!