Аналитическая геометрия на плоскости. Алгебраические линии и плоскости. Уравнения прямой на плоскости

Лекция 7

О размерностях векторных величин

Свойства двойного векторного произведения

1) ;

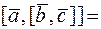
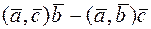2) ;

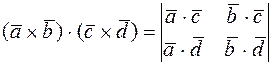3) .

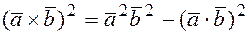В приложениях математики рассматриваются величины, изображаемые векторами: силы, скорости, моменты сил, которые имеют определенные размерности. Напомним основные правила действий с размерностями:

1) сумма имеет ту же размерность, что и слагаемые, и складывать можно векторные величины одинаковых размерностей;

2) при умножении вектора на скалярную величину их размерности перемножаются;

3) модуль векторной величины имеет ту же размерность что и вектор;

4) скалярное и векторное произведение имеют размерность равную произведению размерностей сомножителей.

Цель: Изучить понятия алгебраической линии и алгебраической поверхности, виды уравнений прямой на плоскости и их основные характеристики.

Определение. Уравнение 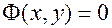называется уравнением линии 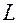на плоскости (относительно заданной системы координат), если этому уравнению удовлетворяют координаты (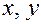) любой точки, лежащей на линии 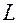, и не удовлетворяют координаты ни одной точки, не лежащей на линиим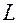. Здесь 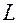- геометрическое место точек, координаты которых удовлетворяют уравнению .

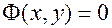Определение: Линия называется алгебраической, если в декартовой прямоугольной системе координат она определяется уравнением 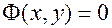, где 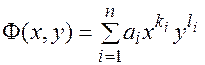- алгебраический полином, 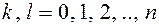- показатели степени все целые неотрицательные числа, 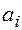- некоторые постоянные.

Определение: Наибольшая из сумм показателей степеней 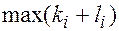называется степенью уравнения или порядком алгебраической линии

Всякая неалгебраическая линия называется трансцендентной.

Определение. Линией -го порядка называется алгебраическая линия, определяемая в декартовой прямоугольной системе координат алгебраическим уравнением -ой степени с двумя неизвестными.

Определение: Алгебраической называется множество, которое в какой-либо декартовой прямоугольной системе координат определяется уравнением 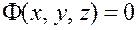, где 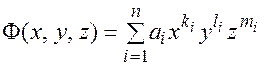- алгебраический полином, 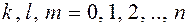- показатели степени все целые неотрицательные числа, 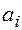- некоторые постоянные.

Определение: Наибольшая из сумм показателей степеней 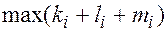называется степенью уравнения или порядком алгебраической поверхности.

Дата добавления: 2013-12-11