Уравнение прямой проходящей через две точки

Уравнение прямой через точку и направляющий вектор

Определение: Всякий ненулевой вектор 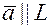с координатами 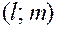параллельный указанной прямой называют направляющим вектором этой прямой (рис. 7.3). Выберем на прямой произвольную точку 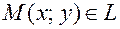и построим вектор 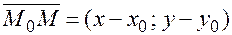. Т.к. векторы 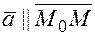, то из условия коллинеарности векторов имеем пропорцию:

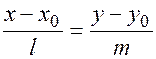(7.4)

Которая дает нам каноническое уравнение прямой.

Рис.7.3

Через любые две несовпадающие точки 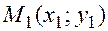, 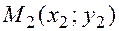можно построить прямую. Пользуясь условием параллельности векторов 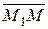и 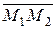(рис.7.4), где 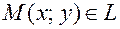получаем:

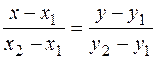(7.5)

уравнение прямой, проходящей через две точк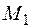ии .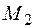

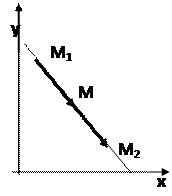
Рис.7.4.

Дата добавления: 2013-12-11