Уравнение прямой с угловым коэффициентом

Замечания.

1. Уравнение 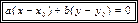называется уравнением прямой, проходящей через точку 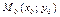перпендикулярно вектору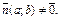

2. Уравнение (13.4) называют общим уравнением прямой. Коэффициенты перед переменными в общем уравнении прямой на плоскости имеют вполне определенный геометрический смысл: они являются координатами нормального вектора прямой.

3. Очевидно, что если в уравнении (13.4) 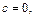то прямая проходит через начало координат.

4. Если в уравнении (13.4) 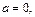то 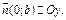В этом случае прямая параллельна оси 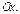Аналогично, если в уравнении (13.4) 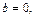то прямая параллельна оси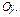

Если в уравнении (13.4) 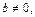то его можно переписать в виде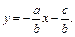Или, обозначая 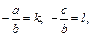в виде:

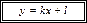(13.7)

Выясним геометрический смысл коэффициентов в уравнении (13.7).

Def. Углом наклона данной прямой к оси 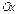называется угол 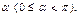на который следует повернуть против хода часовой стрелки ось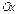до ее совмещения с данной прямой (рис. 13.2, 13.3).

Если прямая параллельна оси 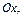то угол наклона этой прямой к оси 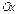принимается равным нулю.

Пусть 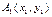и 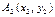- две точки (рис. 13.4) на прямой 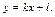Тогда из 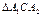имеем:

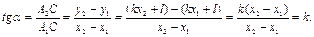(13.8)

Таким образом, коэффициент 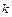в уравнении прямой равен тангенсу угла наклона прямой к оси и называется угловым коэффициентом прямой. В связи с этим, уравнение (13.7) называется уравнением прямой с угловым коэффициентом.

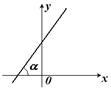Рис. 13.2

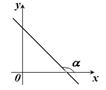Рис. 13.3

Рис. 13.4

Очевидно, что ось прямая, заданная уравнением (13.7), пересекает в точке 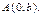Поэтому параметр 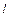в уравнении прямой с угловым коэффициентом равен ординате точки пересечения прямой с осью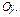

Дата добавления: 2013-12-12