Уравнение Шредингера. Электрон в потенциальной яме

Условие нормировки y-функции.

Чтобы волновая функция являлась объективной характеристикой со­стояния микрочастиц, она должна быть конечной, однозначной, непре­рывной, так как вероятность не может быть больше единицы, не может быть неоднозначной величиной и не может изменяться скачками. Таким образом, состояние микрочастицы полностью определяется волновой функцией. Частица может быть обнаружена в любой точке пространства, в которой волновая функция отлична от нуля.

Основной характеристикой состояния атомов, молекул, элементарных частиц является y -функция. Аналитическое выражение y -функции в каждом конкретном случае можно получить путем решения волнового уравнения – основного урав­нения квантовой механики, предложенного Э. Шредингерам в 1920 г.

Применительно к стационарным состояниям уравнение Шредингера имеет вид:

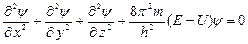. (4.1)

где т – масса частицы; Е и U – ее полная и потенциальная энергии.

Если частица перемещается только вдоль некоторой линии, например, вдоль оси ОХ (одномерный случай), то уравнение Шрёдингера упрощается и принимает вид:

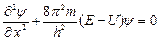(4.2)

Одним из наиболее простых примеров использования уравнения Шрёдингера является решение задачи о движении частицы в одномерной потенциальной яме.

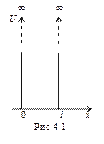Пусть электрон перемещается вдоль оси ОХ только в пределах 0< х<l (рис. 4.1). Это означает, что в указанном интервале y -функция отлична от нуля, а вне интервала (х < 0, х ³ l) равна нулю.

Так как на частицу в выделенном интервале силовые поля не действуют, то ее потенциальная энергия может иметь любое постоянное значение (наиболее удобно принять U =0). Вне этого интервала электрона нет, поэтому следует считать его потенциальную энергию бесконечно большой. На рис. 4.1 показана графическая зависимость U = f(x). Интервал 0< х<l, удовлетворяющий сформулиро­ванным выше условиям, называют одномерной прямоугольной потенциальной ямой с бесконечно высокими стенками. С учетом U =0 уравнение Шрёдингера (4.2) для интервала 0 <х<l имеет вид:

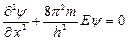. (4.3)

Введем обозначение: 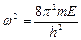, (4.4)

тогда: 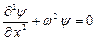(4.5)

Это уравнение аналогично дифференциальному уравнению гармонического колебания, решение которого:

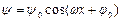, (4.10)

где 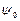–амплитуда волновой функции, 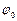–ее начальная фаза. Чтобы найти две постоянные 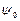и 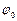, а также возможные значения 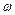или Е, рассмотрим граничные условия:

1) при х = 0 y = 0. Подставляя эти значения в (4.10), получаем

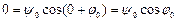
Физический смысл здесь имеет только одно значение: 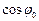= 0, откуда .

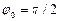2) при х =l y = 0. C учетом 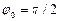из (4.10) имеем:

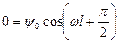
Физический смысл здесь имеет только одно значение:

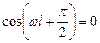, или 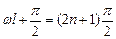, откуда

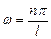, (4.7)

где п – целое число, оно принимает значения 1, 2, 3,...; п ≠ 0, так как в противном случае y = 0 при любом х, что означает отсутствие электрона в потенциальной яме. Число n называют квантовым числом. Из (4.4) находим энергию 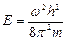, что с учетом (4.7) дает:

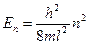. (4.8)

Индекс n при Е показывает, что различным значениям квантового числа n соответствует и разная энергия.

Подставляя w (4.7) в (4.5) и учитывая 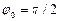, получаем

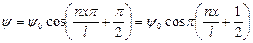. (4.9)

Из (4.8) следует, что решение уравнения Шредингера для электрона в потенциальной яме без каких-либо дополнительных постулатов приводит к дискретным, квантованным значениям энергии: 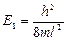; 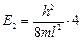и т.д.

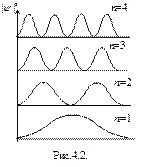
Возведя (4.9) в квадрат, получим плотность вероятности 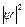нахождения электрона в разных точках потенциальной ямы. На рис.4.2. показана графическая зависимость 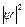от х при разных дискретных состояниях, то есть разных квантовых числах. Как видно из рисунка, электрон может с разной с разной вероятностью находиться в разных местах потенциальной ямы. Есть такие точки, в которых вероятность нахождения электрона вообще равна нулю. Это существенно отличается от представлений классической физики, согласно которым равновероятно нахождение частицы в раз­ных местах потенциальной ямы

Дата добавления: 2013-12-12