В квантовой механике

Линейный гармонический осциллятор

Линейный гармонический осциллятор – это система, совершающая одномерное движение под действием квазиупругой силы. Он является моделью, используемой во многих задачах классической и квантовой теории. Пружинный, физический и математический маятники – примеры классических гармонических осцилляторов. Потенциальная энергия гармонического осциллятора равна:

, (5.1)

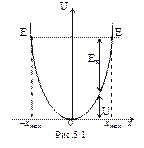
где 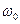— собственная частота колебаний осциллятора, т — масса частицы. Зависимость (5.1) имеет вид параболы (рис. 5.1), т.е. «потенциальная яма» в данном случае является параболической. Амплитуда малых колебаний классического осциллятора определяется его полной энергией Е. В точках с координатами ±х_max полная энергия Е равна потенциальной энергии. Поэтому с классической точки зрения частица не может выйти за пределы области
(– х_max, + х_max).

Гармонический осциллятор в квантовой механике – квантовый осциллятор – опи­сывается уравнением Шредингера (4.2), учитывающим выражение (5.1) для потенциальной энергии. Тогда стационарные состояния квантового осциллятора определяются уравнением Шредингера вида

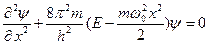(5.2)

где Е — полная энергия осциллятора. В теории дифференциальных уравнений до­казывается, что уравнение (5.2) решается только при собственных значениях энергии

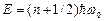(5.3)

где 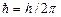. Формула (5.3)показывает, что энергия квантового осциллятора может иметь лишь дискретные значения, т.е. квантуется. Энергия ограничена снизу отличным от нуля минималь­ным значением энергии 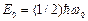. Существование минимальной энергии, назы­ваемой энергией нулевых колебаний, пред­ставляет собой прямое следствие соотношения неопределенностей.

Наличие нулевых колебаний означает, что частица не может находиться на дне «потенциальной ямы», причем этот вывод не зависит от ее формы. В самом деле, «падение на дно ямы» связано с обращением в нуль импульса частицы, а вместе с темиего неопределенности. Тогда неопределенность координаты становится сколь угодно большой, что противоречит, в свою очередь, пребыванию частицы в «потенциальной яме».

Вывод о наличии энергии нулевых колебаний квантового осциллятора противоре­чит выводам классической теории. Например, классическая физика приводит к выводу, что при Т=0 К (Е_к=0) энергия колебательного движения атомов кристалла должна обращаться в нуль. Однако эксперименты по рассеянию света показывают, что при Т®0 колебания атомов в кристалле не прекращаются.

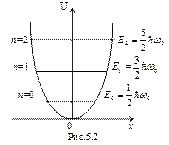
Из формулы (5.3) также следует, что уровни энергии линейного гармонического осциллятора расположены на одинаковых расстояниях друг от друга (рис. 5.2), а имен­но расстояние между соседними энергетическими уровнями равно , причем мини­мальное значение энергии ½.

Квантово-механический расчет показывает, что частицу можно обнаружить за пределами дозволенной области (– х_max, + х_max), в то время как с классической точки зрения она не может выйти за ее пределы. Следовательно, имеется отличная от нуля вероят­ность обнаружить частицу в той области, которая является классически запрещенной. Этот результат (без вывода) демонстрируется на рис.5.3, где приводится квантовая плотность вероятности 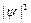обнаружения осциллятора для состояния п =1. Из рисунка следует, что для квантового осциллятора действительно плотность вероятности имеет конечные значения за пределами классически дозволенной области |x|³ х_max, т.е. имеется конечная (но небольшая) вероятность обнаружить частицу за пределами «потенциальной ямы».

Дата добавления: 2013-12-12