Робастные характеристики для оценки среднего арифметического

Квартили и децили.

В дополнение к медиане для характеристики структуры совокупности исчисляются квартили. Квартили - порядковые характеристики, отделяющие четверти ранжированных совокупностей. Децили делят ряд на десять равных частей.

Первый квартиль или нижний отделяет четверть ранжированной совокупности снизу и вычисляется для интервального ряда распределения по формуле:

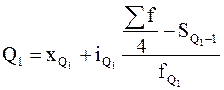
Медиану можно рассматривать как второй квартиль Q₂ = M_e

Верхний квартиль

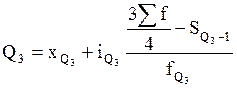
Для дискретного ряда распределения первый и третий квартили исчисляют аналогично медиане, только в этом случае рассматривают соответственно первую и вторую половины всей совокупности для определения средины.

В ряде случаев в изучаемой совокупности имеется небольшое число элементов с чрезвычайно большим или чрезмерно малым значением исследуемого признака.

В этих случаях в дополнение к среднему арифметическому целесообразно вычислить моду и медиану, которые в отличие от среднего не зависят от крайних, не характерных для совокупности значений признака. Мода и медиана относятся к классу так называемых “робастных характеристик”, т.е. не чувствительных к аномальным значениям признака.

Рассмотрим робастные характеристики, применяемые для оценки среднего арифметического:

1. Усеченное среднее арифметическое порядка α 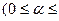½)

Пусть имеем ряд значений признака, упорядоченный в возрастающем порядке

,

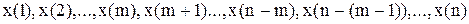упорядоченный в возрастающем порядке.

Пусть первые x(1),...,x(m) - аномально маленькие, а x(n-m+1),...,x(n) - аномально большие.

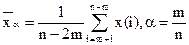
где α - указывает долю отбрасываемых значений признака.

2. Среднее по Виндору

Отличается от усеченного тем, что аномальные значения признака не отбрасываются, а полагаются крайним значениям, принимаемым на обработку.

x(1)=x(2)...=x(m)=x(m+1)

x(n)=x(n-1)=...=x(n-m+1)=x(n-m)

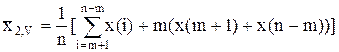
Дата добавления: 2013-12-11