Показатели относительного рассеивания

Приведем пример использования данной формулы для расчета дисперсии

Имеются следующие данные о производительности труда рабочих:

Таблица 36

Табельный номер рабочего	Произведено продукции, шт.
ИТОГО

Произведем следующие расчеты:

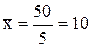шт.

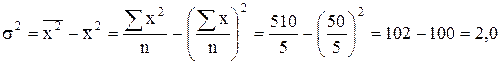
Теперь приведем пример расчета дисперсии в дискретном ряду распределения используя данные нижеследующей таблицы.

Таблица 37.

Произведено продукции 1 рабочим, шт. (х)	Число рабочих, n
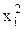
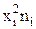
ИТОГО

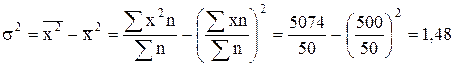
Рассмотрим расчет дисперсии в интервальном ряду распределения.

Порядок расчета дисперсии взвешенной по формуле 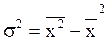будет следующий:

1) определяем среднюю арифметическую ;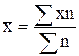

2) возводим в квадрат полученную среднюю ;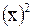

3) возводим в квадрат каждую варианту ряда ;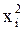

4) умножаем квадраты вариант на частоты ;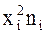

5) суммируем полученные произведения ;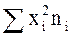

6) делим полученную сумму на сумму весов и получаем средний квадрат признака ;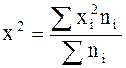

7) определяем разность между средним значением квадратов и квадратом средней арифметической, т.е. дисперсию .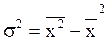

Приведем пример.

Имеются следующие данные о распределении посевной площади сельскохозяйственного предприятия по урожайности пшеницы:

Таблица 38

Урожайность пшеницы, ц/га	Посевная площадь, га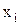
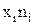
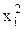
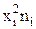
14 - 16
16 - 18
18 - 20
20 - 22
ИТОГО

В подобных примерах прежде всего определяется дискретное значение признака в каждом интервале, а затем применяется метод расчета, указанный выше:

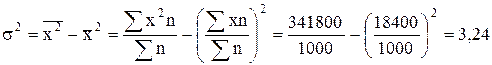
Делая вывод о значении средних величин и показателей вариации можно сказать, что средняя величина отражает тенденцию развития, т.е. действие главных причин (общий уровень развития явления), а среднее квадратическое отклонение измеряет силу воздействия прочих факторов.

Для характеристики меры изменчивости изучаемого признака исчисляются показатели вариации в относительных величинах. Они позволяют сравнивать характер рассеивания в различных распределениях (различные единицы наблюдения одного и того же признака в двух совокупностях, при различных значениях средних, при сравнении разноименных совокупностей). Расчет показателей меры относительного рассеивания осуществляют как отношение абсолютного показателя рассеивания (размах вариации, среднее линейное отклонение, среднее квадратическое отклонение) к средней арифметической, умноженное на 100%.

1. Коэффициент осцилляции отражает относительную изменчивость крайних значений признака вокруг средней.

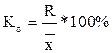
2. Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений от средней величины.

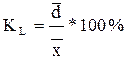
3. Коэффициент вариации.

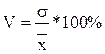
Учитывая, что среднеквадратическое отклонение дает обобщающую характеристику изменчивости всех вариантов совокупности, коэффициент вариации является наиболее распространенным показателем изменчивости, используемым для оценки типичности средних величин. При этом исходят из того, что если V больше 40 %, то это говорит о большой вариации признака в изучаемой совокупности.

Коэффициент вариации характеризует изменчивость признака по отношению к средней. Самые лучшие значения его для устойчивого определения средней до 10%, неплохие до 50%, плохие свыше 50%. Если коэффициент вариации не превышает 33%, то совокупность по рассматриваемому признаку можно считать однородной

4. Квартильное отклонение .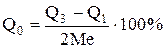

Это показатель дополняет относительные показатели рассеивания. Значение этого показателя больше 50%, а тем более, выше 100% свидетельствует о значительной вариации статистической совокупности. В этом случае вычисленное среднее будет нетипично для характеристики статистической совокупности.

5. Коэффициент дифференциации.

Для характеристики дифференциации статистической совокупности, рассчитывается коэффициент дифференциации по формуле:

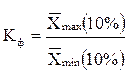
где		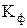коэффициент дифференциации
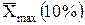
		средняя из 10% максимальных значений признака
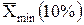
		средняя из 10% минимальных значений признака

Это показатель часто используется для анализа соотношения доходов 10% граждан с самыми высокими доходами и 10% - с самыми низкими, в масштабе страны. В настоящее время в европейских странах этот показатель составляет от 5 до 7. Считается, что если значение этого соотношения достигает 10, то это ведет к высокой социальной напряженности в стране. В России значение этого коэффициента в настоящее время составляет около 14.

Аналогично можно рассчитать соотношение не только 10% групп, но и, к примеру, 5% или 20% групп.

Дата добавления: 2013-12-11