
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Расчет дисперсии и среднего квадратического отклонения по индивидуальным данным и в рядах распределения
|
|
|
|
Основными обобщающими показателями вариации в статистике являются дисперсии и среднее квадратическое отклонение.
Дисперсия - это средняя арифметическая квадратов отклонений каждого значения признака от общей средней. Дисперсия обычно называется средним квадратом отклонений и обозначается 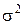 (сигма в квадрате). В зависимости от исходных данных дисперсия может вычисляться по средней арифметической простой или взвешенной:
(сигма в квадрате). В зависимости от исходных данных дисперсия может вычисляться по средней арифметической простой или взвешенной:
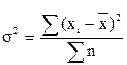 — дисперсия невзвешенная (простая);
— дисперсия невзвешенная (простая);
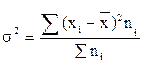 — дисперсия взвешенная.
— дисперсия взвешенная.
Среднее квадратическое отклонение (иногда его называют стандартное отклонение или «стандарт») представляет собой корень квадратный из дисперсии и обозначается σ:
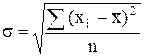 — среднее квадратическое отклонение невзвешенное;
— среднее квадратическое отклонение невзвешенное;
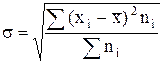 — среднее квадратическое отклонение взвешенное.
— среднее квадратическое отклонение взвешенное.
Среднее квадратическое отклонение - это обобщающая характеристика абсолютных размеров вариации признака в совокупности. Выражается оно в тех же единицах измерения, что и признак (в метрах, тоннах, процентах, гектарах и т.д.).
Среднее квадратическое отклонение является мерилом надежности средней. Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает собой всю представляемую совокупность.
Как известно необходимой предпосылкой корректного использования статистических методов анализа является однородность совокупности. Неоднородность совокупности возникает вследствие значительной вариации значений признака или попадания в совокупность резко выделяющихся, так называемых “аномальных” наблюдений. Для их выявления используется правило трех сигм, которое состоит в том, что “аномальными” будут те варианты, у которых значения анализируемого признака будут выходить за пределы интервала, т.е.:
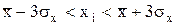
| где | 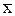
| среднее значение признака |
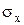
| среднее квадратическое отклонение данного признака | |
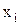
| отдельные значения вариант |
Вычислению среднего квадратического отклонения предшествует расчет дисперсии.
Порядок расчета дисперсии взвешенной:
1) определяют среднюю арифметическую взвешенную:
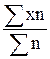 ;
;
2) определяются отклонения вариант от средней 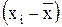 ;
;
3) возводят в квадрат отклонение каждой варианты от средней 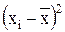 ;
;
4) умножают квадраты отклонений на соответствующие веса (частоты)
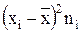 ;
;
5) суммируют полученные произведения
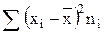 ;
;
6) Полученную сумму делят на сумму весов
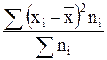 .
.
Приведем пример расчета дисперсии и среднего квадратического отклонения с учетом частот отдельных значений вариант.
Таблица 34.
Произведено продукции одним рабочим, шт.
(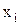 варианта) варианта)
| Число рабочих, 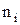
| 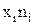
| 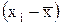
| 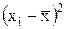
| 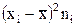
|
| -2 | |||||
| -1 | |||||
| ИТОГО |
Исчислим среднюю арифметическую взвешенную:
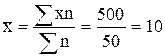 шт.
шт.
Значения отклонений от средней и их квадратов представлены в таблице 6.3. Определим дисперсию:
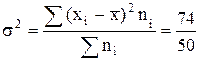 =1,48
=1,48
Среднее квадратическое отклонение будет равно:
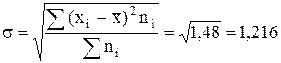 шт.
шт.
Если исходные данные представлены в виде интервального ряда распределения, то сначала надо определить дискретное значение признака, а далее применить тот же метод, что изложен выше.
Покажем расчет дисперсии для интервального ряда на данных о распределении посевной площади сельскохозяйственного предприятия по урожайности пшеницы в следующем примере:
Таблица 35
| Урожайность пшеницы, ц/га | Посевная площадь, га | 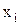
| 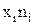
| 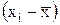
| 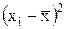
| 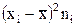
|
| 14 - 16 | -3,4 | 11,56 | ||||
| 16 - 18 | -1,4 | 1,96 | ||||
| 18 - 20 | 0,6 | 0,36 | ||||
| 20 - 22 | 2,6 | 6,76 | ||||
| ИТОГО |
Средняя арифметическая равна:
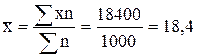 ц с 1га.
ц с 1га.
Исчислим дисперсию:
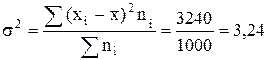
|
|
|
|
|
Дата добавления: 2013-12-11; Просмотров: 1173; Нарушение авторских прав?; Мы поможем в написании вашей работы!