Лекция 2. Кинематика

Аналитические условия равновесия произвольной пространственной системы сил.

Сумма проэкций всех сил на все оси равны нулю, и сумма моментов относительно 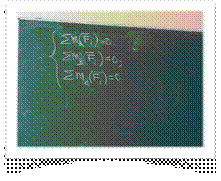всех осей равна нулю.

Для произвольной плоской системы сил, имеем три уравнения равновесия.

Дополнительные формы системы равновесии плоской системы сил.

Закон движения тела - это зависимость положения тела от времени.

Формы задания законов движения. В зависимости от способа определения положения тела существует несколько форм записи закона движения.

Векторная форма закона движения:

Положение тела задается при помощи радиуса- вектора. Радиус вектор имеет начало в начале координат, а конец в точке.

Координатная форма

Положение тела определяется в декартовой системе координат.

Естественная форма

Положение тела задается относительно траектории движения. Этот способ используется когда легко определить траекторию. Для этого вводится естественная координата S. Считаем траекторию координатной осью. Для координаты S выбирается начало и положительное направление, тогда координата определяется длинной дуги. Тогда закон движения имеет вид S=S(t).

Координаты радиуса вектора являются координатами движущейся точки.

Связь между координатным и естественным способом. Рассмотрим изменение естественной координаты за малый промежуток времени и разложим его по проэкциям.

Пример перехода к координатному способу.

Для получения естественного нужно нужно взять производную от каждой координаты. А затем взять интеграл от суммы координат.

Определение скорости точки.

1. Векторный способ

Мгновенная скорость равна производен от дельты радиус вектора. Скорость направлена по касательной к траектории.

2.Координатный способ

Скорость по каждой из координат находится, взятием производной от каждой из координат. Модуль вектора скорости равен корню квадратному из суммы по осям.

При естественном способе скорость равна производной от S.

Ускорение можно определить как скорость изменения скорости:

1. Векторный способ: ускорение находится как производная от скорости или вторая производная от радиус вектора.

2. В координатном способе ускорение есть первая производная от скорости или вторая производная по координате. Модуль ускорения равен квадратному корню из суммы ускорений по осям в квадратах.

3. В естественном способе ускорение раскладывается на две составляющие: нормальное(перпендикулярное касательной) и тангенсальное(направленное по касательной). Модуль нормального ускорения равен частному квадрата скорости и радиуса кривизны траектории, а тангенсальное ускорение выражает изменение скорости по модулю.

Дата добавления: 2013-12-13