Другие модели

ЛЕКЦИЯ 12

Одним из недостатков классической гравитационной модели является то, что объем корреспонденции связывается с характеристиками пары районов (включая транспортное расстояние между ними), взятых в отдельности от других районов. Как отмечается многими исследователями, «привлекательность» района для посещения (или объем прибытия в этот район) может зависеть также от расположения района прибытия среди других районов. Например, район, расположенный в агломерации большого количества других районов посещения, может порождать большую корреспонденцию, чем изолированно расположенный район. Эта идея реализована в моделях семейства конкурирующих центров (competing destinations). Модели конкурирующих центров можно рассматривать как обобщения гравитационной модели, где в выражение (3) включаются дополнительные факторы, например, индекс посещаемости района прибытия, определяемый формулой

(11)

Индекс посещаемости тем больше, чем больше и ближе к району посещения расположены альтернативные районы отправления. Введение этого фактора в модель позволяет моделировать агломерационные эффекты в структуре корреспонденций.

Дальнейшие модификации модели связаны с попыткой учета структуры рассматриваемой системы районов. Например, рассмотрим некоторый регион, где имеются крупные города, окруженные системой прилегающих центров меньшего ранга, каждый из которых окружен прилегающими мелкими районами. В такой системе структурный эффект может проявляться в том, что центр крупного ранга имеет избыточную притягательность для окружающих «подчиненных» центров в иерархии («избыточную» здесь означает «большую, чем это диктуется факторами доступности»). Этот эффект моделируется «ранжированием» районов въезда-выезда по статусу в иерархии и введением соответствующих поправок в индексы посещаемости районов.

Другой важный класс моделей представляют различные модификации модели промежуточных возможностей (intervening opportunities) Стауффер. Модель Стауффера исходит из предположения, что объем корреспонденции между двумя центрами определяется не столько расстоянием между ними, сколько количеством и емкостью альтернативных центров прибытия на пути, соединяющем центры, т.е. количеством альтернативных возможностей посещения. Рассмотрим сначала простую систему с одним центром отправления и рядом центров прибытия, расположенных вдоль одной линии. Пусть Ο — объем отправления, x_n — корреспонденция, v_n — вероятность того, что участник движения остановится в центре n при условии, что центр n достигнут в ходе поездки. Тогда

(12)

т.е. объем корреспонденции в центр n пропорционален произведению вероятности остановки в этом центре на вероятность того, что участник движения не остановился раньше. Для обобщений представляет интерес непрерывный аналог модели, когда места назначения непрерывно распределены вдоль некоторого луча. В непрерывной модели вместо корреспонденций мы будем говорить о плотности корреспонденций x(r), где r — расстояние от центра отправления. Обозначим также: y(r) — количество участников движения, добравшихся до точки r, v(r) — значение плотности распределения вероятности остановки в r при условии, что данная точка достигнута. Тогда, очевидно,

(13)

Из уравнения (13) получаем следующее выражение для плотности корреспонденции:

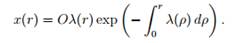(14)

Различные варианты модели конкурирующих возможностей могут быть получены из уравнения (14) путем принятия различных гипотез о виде функции условной плотности вероятности v(r). В применении к расчету корреспонденций в транспортной сети условную вероятность остановки в центре обычно связывают с емкостью центра по прибытию, т.е. количеством мест работы, обслуживания и др.

Обобщение модели на случай многих центров отправления и прибытия сталкивается с трудностью формального определения количества возможностей остановки «по пути» к данному центру. Один из подходов к решению проблемы состоит в ранжировании центров прибытия по удаленности от каждого центра отправления. Все центры, расположенные к центру отправления ближе, чем данный центр (независимо от направления), считаются альтернативными возможностями, «предшествующими» возможности остановки в данном центре. Используя выражение (14) и возвращаясь снова к дискретному описанию центров прибытия-отправления, получаем следующее выражение для корреспонденции:

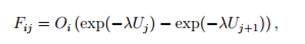(15)

где λ- константа, Uj - кумулятивная емкость по прибытию всех центров, предшествующих (в указанном выше смысле) центру j.

Основное отличие моделей гравитационного типа и моделей промежуточных возможностей состоит в следующем: гравитационные модели основаны на расчете транспортной доступности центров прибытия, рассматриваемых в основном изолированно от альтернативных центров, в то время как модели промежуточных возможностей учитывают взаимное расположение альтернативных возможностей прибытия,

но не учитывают явно фактора транспортной доступности (дальности). В связи с этим предложены различные варианты агрегированных моделей, учитывающие оба указанных фактора. В частности, в предложена объединенная «гравитационно-конкурирующая» (gravity-opportunity) модель энтропийного типа, т.е. основанная на поиске распределения корреспонденций с максимальным статистическим весом. Выражение (15) используется в этой модели в качестве «априорной вероятности» зарождения корреспонденции, фактор транспортной доступности учитывается путем введения «затратного» ограничения (9) в общую систему ограничений энтропийной задачи.

Дата добавления: 2013-12-13